题目内容
11．已知：x2+2x-7=0，那么$\frac{1}{3}{x}^{2}+\frac{2}{3}x-5$=$-\frac{8}{3}$．分析 由题意得：x2+2x=7，等式两边同时乘以$\frac{1}{3}$得$\frac{1}{3}{x}^{2}+\frac{2}{3}x$=$\frac{7}{3}$，然后代入计算即可．
解答 解：∵x2+2x-7=0，
∴x2+2x=7．
∴$\frac{1}{3}{x}^{2}+\frac{2}{3}x$=$\frac{7}{3}$．
∴$\frac{1}{3}{x}^{2}+\frac{2}{3}x-5$=$\frac{7}{3}-5$=$-\frac{8}{3}$．
故答案为：$-\frac{8}{3}$．
点评 本题主要考查的是求代数式的值，利用等式的性质求得$\frac{1}{3}{x}^{2}+\frac{2}{3}x$=$\frac{7}{3}$是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
1．抛物线y=（x-1）2-9与x轴的一个交点为（4，0），另一个交点是（ ）
| A． | （2，0） | B． | （0，-2） | C． | （-2，0） | D． | （0，2） |
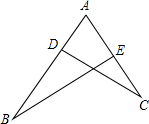如图，点D在AB上，点E在AC上，且AD=$\frac{1}{3}$AC，AE=$\frac{1}{3}$AB．