题目内容
8.某车间每天可以生产甲种零件600个或乙种零件300个或丙种零件500个,这三种零件各一个可以配成一套,现在要用63天的生产中,使生产的三中零件全部配套,这个车间应该对这三种零件的生产各用几天才能生产出来的零件配套.分析 用二元一次方程组解决问题的关键是找到2个合适的等量关系.本题要求三个未知数,但最好设两个未知数.可设生产甲种零件应当用x天,生产乙种零件用y天.则生产丙种零件需z天.那么等量关系为:甲x天生产的零件=乙y天生产的零件=丙z天生产的零件;从其中任取两个等式组成方程组.
解答 解:设生产甲种零件应当用x天,生产乙种零件用y天.则生产丙种零件需z天.
则$\left\{\begin{array}{l}{600x=300y}\\{600x=500z}\\ x+y+z=63\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=15}\\{y=30}\\{z=18}\end{array}\right.$,
答:生产甲种零件应当15天,生产乙种零件应当用30天,生产丙种零件应当用18天.
点评 本题考查了三元一次方程组的应用.在解决实际问题时,若未知量较多,要考虑设三个未知数,但同时应注意,设几个未知数,就要找到几个等量关系列几个方程.

练习册系列答案
 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
19.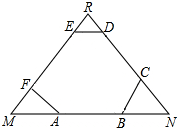 如图,A,B,C,D,E,F是△MNR的三条边上的点,且AB∥DE,BC∥EF,CD∥AF
如图,A,B,C,D,E,F是△MNR的三条边上的点,且AB∥DE,BC∥EF,CD∥AF
(1)∠BAF与∠CDE相等吗?请说明理由;
(2)若∠AFE+∠CDE=230°时,求∠R+∠N的度数.
 如图,A,B,C,D,E,F是△MNR的三条边上的点,且AB∥DE,BC∥EF,CD∥AF
如图,A,B,C,D,E,F是△MNR的三条边上的点,且AB∥DE,BC∥EF,CD∥AF(1)∠BAF与∠CDE相等吗?请说明理由;
(2)若∠AFE+∠CDE=230°时,求∠R+∠N的度数.
13.下列式子正确的是( )
| A. | (x-y)2=x2-xy+y2 | B. | -x(x2-x+1)=-x3-x2-x | ||
| C. | (2ab2)3=6a3b6 | D. | 9x3y2÷(-3x3y)=-3y |
20.一个等腰三角形的两边长分别为2和5,则它的周长为( )
| A. | 7 | B. | 9 | C. | 12 | D. | 9或12 |
18.设甲数为a,乙数为b,甲乙两数的平方和与甲乙两数积的商的代数式是( )
| A. | $\frac{{a}^{2}+{b}^{2}}{ab}$ | B. | (a+b)2ab | C. | (a2+b2)$\frac{a}{b}$ | D. | $\frac{(a+b)^{2}}{ab}$ |
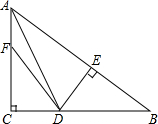 已知:如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于点E,F在AC上,且CF=EB.求证:DB=DF.
已知:如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于点E,F在AC上,且CF=EB.求证:DB=DF.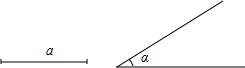 已知一直角边和这条直角边的对角,求作直角三角形(用尺规作图,不写作法,但要保留作图痕迹)
已知一直角边和这条直角边的对角,求作直角三角形(用尺规作图,不写作法,但要保留作图痕迹)