题目内容
3.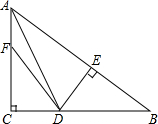 已知:如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于点E,F在AC上,且CF=EB.求证:DB=DF.
已知:如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于点E,F在AC上,且CF=EB.求证:DB=DF.
分析 根据角平分线的性质,可得DE与CD的关系,根据HL,可得△BDE与△FDC间的关系,根据全等三角形的性质,可得答案.
解答 证明:∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,
∴CD=DE.
在Rt△CDF和Rt△EDB中,
$\left\{\begin{array}{l}{CD=DE}\\{CF=BE}\end{array}\right.$,
∴Rt△CDF≌Rt△EDB(HL),
∴DB=DF.
点评 本题考查了全等三角形的判定与性质,角平分线的性质,熟练掌握各性质是解题的关键.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
13.一次函数的图象经过点(2,1)和(-1,-3),则它的解析式为( )
| A. | $y=\frac{3}{4}x-\frac{5}{3}$ | B. | $y=\frac{4}{3}x-\frac{3}{5}$ | C. | $y=\frac{3}{4}x+\frac{3}{5}$ | D. | $y=\frac{4}{3}x-\frac{5}{3}$ |
11.顺次连结对角线垂直的四边形各边中点,所得四边形是( )
| A. | 平行四边形 | B. | 矩形 | C. | 菱形 | D. | 任意四边形 |
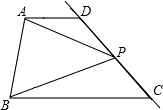 如图梯形ABCD,AD∥BC,点P在直线CD上的运动(不与C,D重合).
如图梯形ABCD,AD∥BC,点P在直线CD上的运动(不与C,D重合).