题目内容
8.点P从距原点8个单位的M点处向原点O方向跳动,第一次跳动到OM的中点M1处,第二次从M1跳到OM1的中点M2处,第三次从点M2跳到OM2的中点M3处,如此不断跳动下去,则第2014次跳到点M2014,则M2014到原点O的距离为$\frac{1}{{2}^{2011}}$.
分析 根据题意,得第一次跳动到OM的中点M3处,即在离原点的$\frac{1}{2}$处,第二次从M3点跳动到M2处,即在离原点的($\frac{1}{2}$)2处,则跳动n次后,即跳到了离原点的$\frac{1}{{2}^{n}}$处,即可根据规律计算出M2014到原点O的距离.
解答 解:由于OM=8,
所有第一次跳动到OM的中点M3处时,OM3=$\frac{1}{2}$OM=4,
同理第二次从M3点跳动到M2处,即在离原点的($\frac{1}{2}$)2×8=2处,
同理跳动n次后,即跳到了离原点的$\frac{1}{{2}^{n}}$×8处,
∴第2014次跳到点M2014,则M2014到原点O的距离为:$\frac{1}{{2}^{2014}}$×8=$\frac{{2}^{3}}{{2}^{2014}}$=$\frac{1}{{2}^{2011}}$.
故答案为:$\frac{1}{{2}^{2011}}$.
点评 本题主要考查点的坐标,这是一道找规律的题目,这类题型在中考中经常出现.解答本题的关键是找出各个点跳动的规律,此题比较简单.

练习册系列答案
相关题目
18.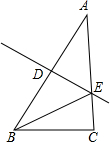 如图,在△ABC中,AB的垂直平分线分别交AB,AC于D,E两点,且AC=10,BC=4,则△BCE的周长为( )
如图,在△ABC中,AB的垂直平分线分别交AB,AC于D,E两点,且AC=10,BC=4,则△BCE的周长为( )
 如图,在△ABC中,AB的垂直平分线分别交AB,AC于D,E两点,且AC=10,BC=4,则△BCE的周长为( )
如图,在△ABC中,AB的垂直平分线分别交AB,AC于D,E两点,且AC=10,BC=4,则△BCE的周长为( )| A. | 6 | B. | 14 | C. | 18 | D. | 24 |
16.若代数式$\frac{\sqrt{2-x}}{1+x}$有意义,则x的取值范围是( )
| A. | x≥-2且x≠-1 | B. | x>-2且x≠-1 | C. | x≤2且x≠-1 | D. | x<2且x≠-1 |
3.下列四个函数图象中,当x>0时,y随x的增大而减小的是( )
| A. | 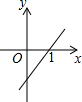 | B. | 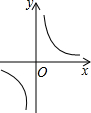 | C. | 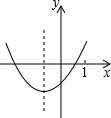 | D. | 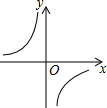 |
17.一水果经销商购进了A,B两种水果各10箱,分配给他的甲、乙两个零售店(分别简称甲店、乙店)销售,预计每箱水果的盈利情况如下表:
(1)如果甲、乙两店各配货10箱,其中A种水果两店各5箱,B种水果两店各5箱,请你计算出经销商能盈利多少元?
(2)在甲、乙两店各配货10箱(按整箱配送),且保证乙店盈利不小于100元的条件下,请你设计出使水果经销商盈利最大的配货方案,并求出最大盈利为多少?
| A种水果/箱 | B种水果/箱 | |
| 甲店 | 11元 | 17元 |
| 乙店 | 9元 | 13元 |
(2)在甲、乙两店各配货10箱(按整箱配送),且保证乙店盈利不小于100元的条件下,请你设计出使水果经销商盈利最大的配货方案,并求出最大盈利为多少?
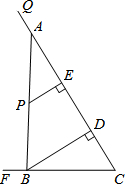 如图,tan∠QCF=2,点E在射线CQ上,CE=12.点P是∠QCF内一点,PE⊥QC于点E,PE=4.在射线CQ上取一点A,连AP并延长交射线CF于点B,作BD⊥QC于点D.
如图,tan∠QCF=2,点E在射线CQ上,CE=12.点P是∠QCF内一点,PE⊥QC于点E,PE=4.在射线CQ上取一点A,连AP并延长交射线CF于点B,作BD⊥QC于点D.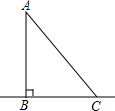 某小区的A处有一个凉亭,道路AB、BC、AC两两相交于点A、B、C,并且道路AB与道路BC相互垂直.如图所示,已知A和B之间的距离为20m,若有两个小朋友在与点B相距10m点D处玩耍,玩累了他们沿不同的路线到凉亭A处喝水休息,已知D→B→A与D→C→A的路程相等,求A与C之间的距离.
某小区的A处有一个凉亭,道路AB、BC、AC两两相交于点A、B、C,并且道路AB与道路BC相互垂直.如图所示,已知A和B之间的距离为20m,若有两个小朋友在与点B相距10m点D处玩耍,玩累了他们沿不同的路线到凉亭A处喝水休息,已知D→B→A与D→C→A的路程相等,求A与C之间的距离.