题目内容
12.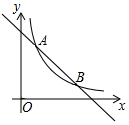 如图,一次函数y=-x+5的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象交于A(1,n)和B两点.
如图,一次函数y=-x+5的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象交于A(1,n)和B两点.(1)求反比例函数的解析式;
(2)在第一象限内,当一次函数y=-x+5的值大于反比例函数y=$\frac{k}{x}$(k≠0)的值时,写出自变量x的取值范围.
分析 (1)首先求出点A的坐标,进而即可求出反比例函数系数k的值;
(2)联立反比例函数和一次函数解析式,求出交点B的坐标,结合图形即可求出x的取值范围.
解答 解:(1)∵一次函数y=-x+5的图象过点A(1,n),
∴n=-1+5,
∴n=4,
∴点A坐标为(1,4),
∵反比例函数y=$\frac{k}{x}$(k≠0)过点A(1,4),
∴k=4,
∴反比例函数的解析式为y=$\frac{4}{x}$;
(2)联立$\left\{\begin{array}{l}{y=-x+5}\\{y=\frac{4}{x}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=1}\\{y=4}\end{array}\right.$或$\left\{\begin{array}{l}{x=4}\\{y=1}\end{array}\right.$,
即点B的坐标(4,1),
若一次函数y=-x+5的值大于反比例函数y=$\frac{k}{x}$(k≠0)的值,
则1<x<4.
点评 本题主要考查了反比例函数与一次函数的交点问题,解答本题的关键是求出A点和B点的坐标,此题难度不大.

练习册系列答案
相关题目
3.下列四个函数图象中,当x>0时,y随x的增大而减小的是( )
| A. | 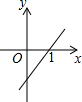 | B. | 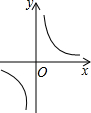 | C. | 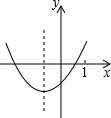 | D. | 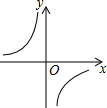 |
17.一水果经销商购进了A,B两种水果各10箱,分配给他的甲、乙两个零售店(分别简称甲店、乙店)销售,预计每箱水果的盈利情况如下表:
(1)如果甲、乙两店各配货10箱,其中A种水果两店各5箱,B种水果两店各5箱,请你计算出经销商能盈利多少元?
(2)在甲、乙两店各配货10箱(按整箱配送),且保证乙店盈利不小于100元的条件下,请你设计出使水果经销商盈利最大的配货方案,并求出最大盈利为多少?
| A种水果/箱 | B种水果/箱 | |
| 甲店 | 11元 | 17元 |
| 乙店 | 9元 | 13元 |
(2)在甲、乙两店各配货10箱(按整箱配送),且保证乙店盈利不小于100元的条件下,请你设计出使水果经销商盈利最大的配货方案,并求出最大盈利为多少?
5.下列图形中国,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
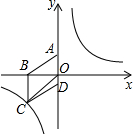 如图,将菱形ABCD放置在平面直角坐标系中,已知A(0,3).B(-4,0)
如图,将菱形ABCD放置在平面直角坐标系中,已知A(0,3).B(-4,0)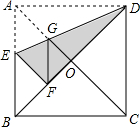 如图,在正方形纸片ABCD中,对角线AC,BD交于点O,折叠正方形ABCD使AD落在BD上,点A恰好与BD上的点F重合,展开后,折痕DE分别交AB,AC于点E、G,连接GF,有下列结论:①∠AGD=122.5°;②$\frac{AD}{AE}=2$;③BE=2OG;④DG=2EG;⑤AC-AD=EF,其中正确的序号是( )
如图,在正方形纸片ABCD中,对角线AC,BD交于点O,折叠正方形ABCD使AD落在BD上,点A恰好与BD上的点F重合,展开后,折痕DE分别交AB,AC于点E、G,连接GF,有下列结论:①∠AGD=122.5°;②$\frac{AD}{AE}=2$;③BE=2OG;④DG=2EG;⑤AC-AD=EF,其中正确的序号是( )