题目内容
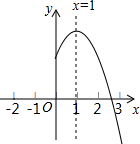 二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,有如下结论:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,有如下结论:①abc<0;②a-b+c>0;③b2>4ac;④3a-2b+c<0,则正确的结论是( )
| A、①②③ | B、①③④ |
| C、②③④ | D、①②③④ |
考点:二次函数图象与系数的关系
专题:数形结合
分析:由抛物线开口方向得a<0,由抛物线的对称轴为直线x=-
=1得b=-2a>0,由抛物线与y轴的交点位置得c>0,则可对①进行判断;利用抛物线的对称性得到抛物线与x轴的另一个交点在(0,0)与(-1,0)之间,则当x=-1时,y<0,即a-b+c<0,于是可对②进行判断;利用抛物线与x轴的交点个数可对③进行判断;利用b=-2a得3a-2b+c=7a+c,而a-b+c<0,即3a+c<0,则3a-2b+c=3a+c+4a<0,于是可对④进行判断.
| b |
| 2a |
解答:解:∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴为直线x=-
=1,
∴b=-2a>0,
∵抛物线与y轴的交点在x轴上方,
∴c>0,
∴abc<0,所以①正确;
∵抛物线与x轴的一个交点在(2,0)与(3,0)之间,而对称轴为直线x=1,
∴抛物线与x轴的另一个交点在(0,0)与(-1,0)之间,
∴当x=-1时,y<0,
∴a-b+c<0,所以②错误;
∵抛物线与x轴有2个交点,
∴△=b2-4ac>0,即b2>4ac,所以③正确
∵b=-2a,
∴3a-2b+c=3a+4a+c=7a+c,
∵a-b+c<0,即3a+c<0,
∴3a-2b+c=7a+c=3a+c+4a<0,所以④正确.
故选B.
∴a<0,
∵抛物线的对称轴为直线x=-
| b |
| 2a |
∴b=-2a>0,
∵抛物线与y轴的交点在x轴上方,
∴c>0,
∴abc<0,所以①正确;
∵抛物线与x轴的一个交点在(2,0)与(3,0)之间,而对称轴为直线x=1,
∴抛物线与x轴的另一个交点在(0,0)与(-1,0)之间,
∴当x=-1时,y<0,
∴a-b+c<0,所以②错误;
∵抛物线与x轴有2个交点,
∴△=b2-4ac>0,即b2>4ac,所以③正确
∵b=-2a,
∴3a-2b+c=3a+4a+c=7a+c,
∵a-b+c<0,即3a+c<0,
∴3a-2b+c=7a+c=3a+c+4a<0,所以④正确.
故选B.
点评:本题考查了二次函数图象与系数的关系:对于二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右;常数项c决定抛物线与y轴交点:抛物线与y轴交于(0,c);抛物线与x轴交点个数由△决定:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
相关题目
-9的倒数是( )
A、-
| ||
B、
| ||
| C、-9 | ||
| D、9 |
现在网购越来越多地成为人们的一种消费方式,刚刚过去的2014年的“双11”网上促销活动中,天猫和淘宝的支付交易额突破571亿元,将571亿元用科学记数法表示为( )
| A、5.71×108 |
| B、5.71×1010 |
| C、5.71×109 |
| D、0.571×1011 |
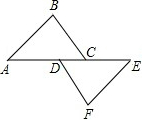 如图,点A、D、C、E在同一条直线上,AB∥EF,AB=EF,∠B=∠F,AE=10,AC=7,则CD的长为( )
如图,点A、D、C、E在同一条直线上,AB∥EF,AB=EF,∠B=∠F,AE=10,AC=7,则CD的长为( )| A、5.5 | B、4 | C、4.5 | D、3 |
 如图,AD=BC,AB=DC.求证:∠A+∠D=180°.
如图,AD=BC,AB=DC.求证:∠A+∠D=180°.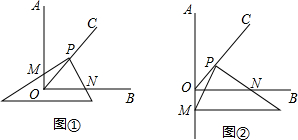
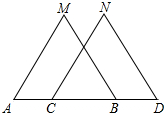 如图,已知A、B、C、D四点在同一直线上,AM=CN,BM=DN,∠M=∠N,
如图,已知A、B、C、D四点在同一直线上,AM=CN,BM=DN,∠M=∠N,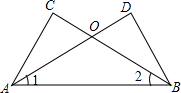 已知:如图,∠1=∠2,∠C=∠D.求证:
已知:如图,∠1=∠2,∠C=∠D.求证: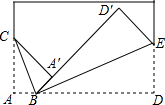 如图,将长方形纸片的一角折叠,使顶点A落在点A′处,折痕CB;再将长方形纸片的另一角折叠,使顶点D落在点D′处,D′在BA′的延长线上,折痕EB.
如图,将长方形纸片的一角折叠,使顶点A落在点A′处,折痕CB;再将长方形纸片的另一角折叠,使顶点D落在点D′处,D′在BA′的延长线上,折痕EB.