题目内容
20.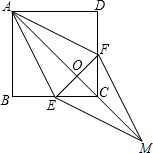 如图,在正方形ABCD中,点E、F分别在BC和CD上,AE=AF,AO=OM,下列说法错误的是( )
如图,在正方形ABCD中,点E、F分别在BC和CD上,AE=AF,AO=OM,下列说法错误的是( )| A. | AE=AF | B. | AM⊥EF | C. | DF=FC | D. | AF=FM |
分析 根据正方形的性质可得AB=AD,∠B=∠D=90°,然后利用“HL”证明Rt△ABE和Rt△ADF全等,求出CE=CF,然后利用“边边边”证明△AEC和△AFC全等,根据全等三角形对应角相等可得∠EAC=∠FAC,再根据等腰三角形三线合一的性质可得AC垂直平分EF,根据线段垂直平分线上的点到两端点的距离相等可得EM=FM,再判断出EF垂直平分AM,根据线段垂直平分线上的点到两端点的距离相等可得AE=EM,然后根据四条边都相等的四边形是菱形,继而证得AM⊥EF.
解答 解:在正方形ABCD中,AB=AD,∠B=∠D=90°,
在Rt△ABE和Rt△ADF中,
$\left\{\begin{array}{l}{AE=AF}\\{AB=AD}\end{array}\right.$,
∴Rt△ABE≌Rt△ADF(HL),
∴BE=DF;
∵BC=CD,BE=DF,
∴BC-BE=CD-CF,
即CE=CF,
在△AEC和△AFC中,
$\left\{\begin{array}{l}{AE=AF}\\{AC=AC}\\{CE=CF}\end{array}\right.$,
∴△AEC≌△AFC(SSS),
∴∠EAC=∠FAC,
又∵AE=AF,
∴AC垂直平分EF,
∴EM=FM,
∵OM=OA,
∴EF垂直平分AM,
∴AE=EM,
∴AE=EM=FM=AF,故A、D正确;
∴四边形AEMF是菱形,
∴AM⊥EF;故B正确.
故选C.
点评 此题考查了正方形的性质,全等三角形的判定与性质以及菱形的判定与性质.注意证得四边形AEMF是菱形是解此题的关键.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
11.下列是最简分式的是( )
| A. | $\frac{ab}{a^2}$ | B. | $\frac{4x-1}{4x}$ | C. | $\frac{1+a}{1-{a}^{2}}$ | D. | $\frac{4y}{6x}$ |
8.已知一条抛物线经过E(0,10),F(2,2),G(4,2),H(3,1)四点,选择其中两点用待定系数法能求出抛物线解析式的为( )
| A. | E,F | B. | E,G | C. | E,H | D. | F,G |
15.下列计算正确的是( )
| A. | 2x2•3x3=6x3 | B. | 2x2+3x3=5x5 | ||
| C. | (-3x2)•(-3x2)=9x4 | D. | $\frac{5}{4}{x^m}•\frac{2}{5}{x^n}=\frac{1}{2}{x^{mn}}$ |
5.为了比较某校同学汉字听写谁更优秀,语文老师随机抽取了10次听写情况,发现甲乙两人平均成绩一样,甲、乙的方差分别为2.7和3.2,则下列说法正确的是( )
| A. | 甲的发挥更稳定 | B. | 乙的发挥更稳定 | ||
| C. | 甲、乙同学一样稳定 | D. | 无法确定甲、乙谁更稳定 |
12.下列命题为假命题的是( )
| A. | 全等三角形对应边相等,对应角相等 | |
| B. | 角平分线上的点到角两边距离相等 | |
| C. | 到线段两端点距离相等的点在这条线段的垂直平分线上 | |
| D. | 等腰三角形一边上的中线、高线和所对角的角平分线互相重合 |
 小丽做了一个画角平分线的仪器(图1),其中AB=AC,BD=DC.将仪器上的点A与∠PQR的顶点Q重合,调整AB和AC的位置,使它们分别落在∠PQR的两边上,过点A、D的射,线就是∠PRQ的角平分线(图2).此仪器的画图原理是:根据仪器结构,可得△ABD≌△ACD,这样就有∠BAD=∠CAD.其中,△ABD≌△ACD的依据是( )
小丽做了一个画角平分线的仪器(图1),其中AB=AC,BD=DC.将仪器上的点A与∠PQR的顶点Q重合,调整AB和AC的位置,使它们分别落在∠PQR的两边上,过点A、D的射,线就是∠PRQ的角平分线(图2).此仪器的画图原理是:根据仪器结构,可得△ABD≌△ACD,这样就有∠BAD=∠CAD.其中,△ABD≌△ACD的依据是( )