题目内容
16.阅读下面材料:小丁在研究数学问题时遇到一个定义:对于排好顺序的三个数:x1,x2,x3,称为数列x1,x2,x3.计算|x1|,$\frac{|{x}_{1}+{x}_{2}|}{2}$,$\frac{|{x}_{1}+{x}_{2}+{x}_{3}|}{3}$,将这三个数的最小值称为数列x1,x2,x3的价值.例如,对于数列2,-1,3,因为|2|=2,$\frac{|2+(-1)|}{2}$=$\frac{1}{2}$,$\frac{|2+(-1)+3|}{3}$=$\frac{4}{3}$,所以数列2,-1,3的价值为$\frac{1}{2}$.
小丁进一步发现:当改变这三个数的顺序时,所得到的数列都可以按照上述方法计算其相应的价值.如数列-1,2,3的价值为$\frac{1}{2}$;数列3,-1,2的价值为1;….经过研究,小丁发现,对于“2,-1,3”这三个数,按照不同的排列顺序得到的不同数列中,价值的最小值为$\frac{1}{2}$.根据以上材料,回答下列问题:
(1)数列-4,-3,2的价值为$\frac{5}{3}$;
(2)将“-4,-3,2”这三个数按照不同的顺序排列,可得到若干个数列,这些数列的价值的最小值为$\frac{1}{2}$,取得价值最小值的数列为-3,2,-4或2,-3,-4(写出一个即可);
(3)将2,-9,a(a>1)这三个数按照不同的顺序排列,可得到若干个数列.若这些数列的价值的最小值为1,则a的值为11或4.
分析 (1)根据上述材料给出的方法计算其相应的价值即可;
(2)按照三个数不同的顺序排列算出价值,由计算可以看出,要求得这些数列的价值的最小值;只有当前两个数的和的绝对值最小,最小只能为|-3+2|=1,由此得出答案即可;
(3)分情况算出对应的数值,建立方程求得a的数值即可.
解答 解:(1)因为|-4|=4,|$\frac{-4-3}{2}$|=3.5,|$\frac{-4-3+2}{3}$|=$\frac{5}{3}$,
所以数列-4,-3,2的价值为$\frac{5}{3}$,
故答案为:$\frac{5}{3}$;
(2)数列的价值的最小值为|$\frac{-3+2}{2}$|=$\frac{1}{2}$,
数列可以为:-3,2,-4,或2,-3,-4,
故答案为:$\frac{1}{2}$;-3,2,-4,或2,-3,-4;
(3)当|$\frac{2+a}{2}$|=1,则a=0,不合题意;
当|$\frac{-9+a}{2}$|=1,则a=11;
当|$\frac{2-9+a}{3}$|=1,则a=4.
故答案为:11或4.
点评 此题考查了算术平均数的定义以及数字的变化规律,理解运算的方法是解决问题的关键.

练习册系列答案
相关题目
5.计算(c2)n•(cn+1)2等于( )
| A. | c4n+2 | B. | c4n2+2 | C. | x2+2 | D. | c3n+4 |
6.下列实数中,是负数的是( )
| A. | -$\sqrt{2}$ | B. | 2.5 | C. | 0 | D. | $\frac{5}{7}$ |
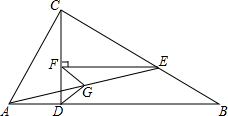 己知:如图,在△ABC中,∠ACB=90°,CD⊥AB垂足为D,E是CB上一点,且CE=AC,EF⊥CD,垂足为F.
己知:如图,在△ABC中,∠ACB=90°,CD⊥AB垂足为D,E是CB上一点,且CE=AC,EF⊥CD,垂足为F.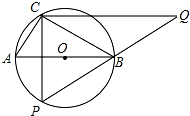 如图,在⊙O上有定点C和动点P,位于直径AB的两侧,过点C作CP的垂线与PB的延长线交于点Q.已知⊙O的直径为5,tan∠ABC=$\frac{3}{4}$,则CQ的最大值为$\frac{20}{3}$.
如图,在⊙O上有定点C和动点P,位于直径AB的两侧,过点C作CP的垂线与PB的延长线交于点Q.已知⊙O的直径为5,tan∠ABC=$\frac{3}{4}$,则CQ的最大值为$\frac{20}{3}$.