题目内容
13. 直角三角形的一个角是60°,用四个这样的直角三角形拼成如图所示的正方形ABCD,若正方形EFGH的边长是$\sqrt{3}$-1,则正方形ABCD的边长是2.
直角三角形的一个角是60°,用四个这样的直角三角形拼成如图所示的正方形ABCD,若正方形EFGH的边长是$\sqrt{3}$-1,则正方形ABCD的边长是2.
分析 设BF=x,由已知条件可得∠BAF=30°,所以AB=2x,由勾股定理可计算出AF=$\sqrt{3}$x,因为AF=EF+x,则可建立关于x的方程,所以x的值可求出,进而可求出正方形ABCD的边长.
解答 解:
∵四边形ABCD是正方形,
∴∠ABC=90°,
∵∠ABF=60°,
∴∠BAF=30°,
设BF=x,AB=2x,
∴AF=$\sqrt{A{B}^{2}-B{F}^{2}}$=$\sqrt{3}$x,
∵AF=AE+EF=$\sqrt{3}$-1+x,
∴$\sqrt{3}$x=$\sqrt{3}$-1+x,
解得:x=1,
∴AB=2,
即正方形ABCD的边长是2,
故答案为:2.
点评 本题考查了正方形的性质、勾股定理的运用以及在直角三角形中30°所对直角边时斜边一半性质的运用,题目的综合性较强,难度中等,是一道不错的中考题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在半⊙O中,P为直径AB上的一个动点,点C,D为半圆的三等分点,若AB=12,则图中阴影部分的面积为6π.
如图,在半⊙O中,P为直径AB上的一个动点,点C,D为半圆的三等分点,若AB=12,则图中阴影部分的面积为6π. 在同一直角坐标系中,一次函数y1=k1x+b与正比例函数y2=k2x的图象如图所示,则满足y1≥y2的x取值范围是x≤-2.
在同一直角坐标系中,一次函数y1=k1x+b与正比例函数y2=k2x的图象如图所示,则满足y1≥y2的x取值范围是x≤-2. 如图,OA表示南偏西20°方向的一条射线,∠AOB=90°,那么OB的方向可表示为南偏东70°.
如图,OA表示南偏西20°方向的一条射线,∠AOB=90°,那么OB的方向可表示为南偏东70°.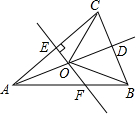 如图,在△ABC中,AB=AC,点D是BC的中点,AC的垂直平分线分别交AC,AD,AB于点E,O,F.
如图,在△ABC中,AB=AC,点D是BC的中点,AC的垂直平分线分别交AC,AD,AB于点E,O,F.