题目内容
1.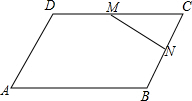 如图,在平行四边形ABCD中,点M是边CD中点,点N是边BC上的点,且$\frac{CN}{BN}$=$\frac{1}{2}$.设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,那么$\overrightarrow{MN}$可用$\overrightarrow{a}$、$\overrightarrow{b}$表示为$\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{3}$$\overrightarrow{b}$.
如图,在平行四边形ABCD中,点M是边CD中点,点N是边BC上的点,且$\frac{CN}{BN}$=$\frac{1}{2}$.设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,那么$\overrightarrow{MN}$可用$\overrightarrow{a}$、$\overrightarrow{b}$表示为$\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{3}$$\overrightarrow{b}$.
分析 首先由四边形ABCD是平行四边形,求得$\overrightarrow{DC}$=$\overrightarrow{AB}$=$\overrightarrow{a}$,又由点M是边CD中点,点N是边BC上的点,且$\frac{CN}{BN}$=$\frac{1}{2}$,求得$\overrightarrow{MC}$与$\overrightarrow{NC}$,再利用三角形法则求解即可求得答案.
解答 解:∵四边形ABCD是平行四边形,
∴$\overrightarrow{DC}$=$\overrightarrow{AB}$=$\overrightarrow{a}$,
∵点M是边CD中点,点N是边BC上的点,且$\frac{CN}{BN}$=$\frac{1}{2}$,
∴$\overrightarrow{MC}$=$\frac{1}{2}$$\overrightarrow{DC}$=$\frac{1}{2}$$\overrightarrow{a}$,$\overrightarrow{NC}$=$\frac{1}{3}$$\overrightarrow{BC}$=$\frac{1}{3}$$\overrightarrow{b}$,
∴$\overrightarrow{MN}$=$\overrightarrow{MC}$-$\overrightarrow{NC}$=$\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{3}$$\overrightarrow{b}$.
故答案为:$\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{3}$$\overrightarrow{b}$.
点评 此题考查了平面向量的知识.注意掌握平行四边形法则与三角形法则的应用是解此题的关键.

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案 如图,是我市几个旅游景点的大致位置示意图,如果用(-1,0)表示雨花塘的位置,用(1,5)表示杏花公园的位置,那么天鹅湖的位置可以表示为( )
如图,是我市几个旅游景点的大致位置示意图,如果用(-1,0)表示雨花塘的位置,用(1,5)表示杏花公园的位置,那么天鹅湖的位置可以表示为( )| A. | A(3,3) | B. | (-2,-3) | C. | (-3,-3) | D. | (-2,-2) |
| A. | 2与3之间 | B. | 3与4之间 | C. | 4与5之间 | D. | 5与6之间 |
 如图是某几何体的三视图,该几何体是( )
如图是某几何体的三视图,该几何体是( )| A. | 圆锥 | B. | 三棱柱 | C. | 圆柱 | D. | 三棱锥 |
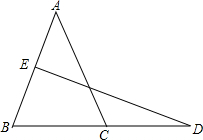 已知:如图,在△ABC中,AB=AC=6,BC=4,AB的垂直平分线交AB于点E,交BC的延长线于点D.
已知:如图,在△ABC中,AB=AC=6,BC=4,AB的垂直平分线交AB于点E,交BC的延长线于点D.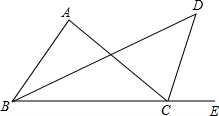 如图,△ABC中,∠A=90°,∠ABC的平分线与∠ACE的平分线相交于点D,求∠D的度数.
如图,△ABC中,∠A=90°,∠ABC的平分线与∠ACE的平分线相交于点D,求∠D的度数. 如图,平面直角坐标系中,O是坐标原点,抛物线C1:y=ax2经过点(1,-1).
如图,平面直角坐标系中,O是坐标原点,抛物线C1:y=ax2经过点(1,-1).