题目内容
9. 如图,菱形AB1C1D1的边长为1,∠B1=60°;作AD2⊥B1C1于点D2,以AD2为一边,做第二个菱形AB2C2D2,使∠B2=60°;作AD3⊥B2C2于点D3,以AD3为一边做第三个菱形AB3C3D3,使∠B3=60°…则AD2=$\frac{\sqrt{3}}{2}$,依此类推这样做的第n个菱形ABnCnDn的边ADn的长是($\frac{\sqrt{3}}{2}$)n-1.
如图,菱形AB1C1D1的边长为1,∠B1=60°;作AD2⊥B1C1于点D2,以AD2为一边,做第二个菱形AB2C2D2,使∠B2=60°;作AD3⊥B2C2于点D3,以AD3为一边做第三个菱形AB3C3D3,使∠B3=60°…则AD2=$\frac{\sqrt{3}}{2}$,依此类推这样做的第n个菱形ABnCnDn的边ADn的长是($\frac{\sqrt{3}}{2}$)n-1.
分析 在△AB1D2中利用三角函数的定义计算出AD2=$\frac{\sqrt{3}}{2}$,再根据菱形的性质得AB2=AD2=$\frac{\sqrt{3}}{2}$,则利用三角函数的定义得到AD3=($\frac{\sqrt{3}}{2}$)2,同理可得AD4=($\frac{\sqrt{3}}{2}$)3,利用此变换规律得到ADn=($\frac{\sqrt{3}}{2}$)n-1.
解答 解:在△AB1D2中,∵sinB1=$\frac{A{D}_{2}}{A{B}_{1}}$,
∴AD2=1×sin60°=$\frac{\sqrt{3}}{2}$,
∵四边形AB2C2D2为菱形,
∴AB2=AD2=$\frac{\sqrt{3}}{2}$,
在△AB2D3中,∵sinB2=$\frac{A{D}_{3}}{A{B}_{2}}$,
∴AD3=$\frac{\sqrt{3}}{2}$×sin60°=($\frac{\sqrt{3}}{2}$)2,
同理可得AD4=($\frac{\sqrt{3}}{2}$)3,
∴第n个菱形ABnCnDn的边ADn的长为($\frac{\sqrt{3}}{2}$)n-1.
故答案为$\frac{\sqrt{3}}{2}$,($\frac{\sqrt{3}}{2}$)n-1.
点评 本题考查了菱形的性质:菱形具有平行四边形的一切性质;菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.菱形的面积等于对角线乘积的一半.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
14.已知两点P1(1,y1),P2(5,y2)在反比例函数y=$\frac{5}{x}$的图象上,下列结论正确的是( )
| A. | 0<y1<y2 | B. | 0<y2<y1 | C. | y1<y2<0 | D. | y2<y1<0 |
1.二次函数y=2x2-2x+m(0<m<$\frac{1}{2}$),如果当x=a时,y<0,那么当x=a-1时,函数值y的取值范围为( )
| A. | y<0 | B. | 0<y<m | C. | m<y<m+4 | D. | y>m |
18.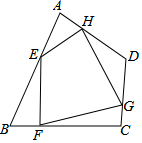 如图,任意四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA上的点,对于四边形EFGH的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是( )
如图,任意四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA上的点,对于四边形EFGH的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是( )
 如图,任意四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA上的点,对于四边形EFGH的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是( )
如图,任意四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA上的点,对于四边形EFGH的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是( )| A. | 当E,F,G,H是各边中点,且AC=BD时,四边形EFGH为菱形 | |
| B. | 当E,F,G,H是各边中点,且AC⊥BD时,四边形EFGH为矩形 | |
| C. | 当E,F,G,H不是各边中点时,四边形EFGH可以为平行四边形 | |
| D. | 当E,F,G,H不是各边中点时,四边形EFGH不可能为菱形 |
 如图,四边形ABCD中,∠A=∠ABC=90°,AD=10cm,BC=30cm,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.
如图,四边形ABCD中,∠A=∠ABC=90°,AD=10cm,BC=30cm,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.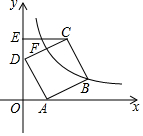 如图,正方形ABCD的两个顶点A,D分别在x轴和y轴上,CE⊥y轴于点E,OA=2,∠ODA=30°.若反比例函数y=$\frac{k}{x}$的图象过CE的中点F,则k的值为2$\sqrt{3}$+6.
如图,正方形ABCD的两个顶点A,D分别在x轴和y轴上,CE⊥y轴于点E,OA=2,∠ODA=30°.若反比例函数y=$\frac{k}{x}$的图象过CE的中点F,则k的值为2$\sqrt{3}$+6.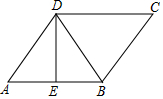 如图,在?ABCD中,D在AB的垂直平分线上,且?ABCD的周长为42cm,△BCD的周长比?ABCD的周长少12cm,则AB=12cm,S?ABCD=36$\sqrt{5}$cm2.
如图,在?ABCD中,D在AB的垂直平分线上,且?ABCD的周长为42cm,△BCD的周长比?ABCD的周长少12cm,则AB=12cm,S?ABCD=36$\sqrt{5}$cm2.