题目内容
1．二次函数y=2x2-2x+m（0＜m＜$\frac{1}{2}$），如果当x=a时，y＜0，那么当x=a-1时，函数值y的取值范围为（ ）| A． | y＜0 | B． | 0＜y＜m | C． | m＜y＜m+4 | D． | y＞m |
分析 画出草图，易求得抛物线对称轴，可以找出a的大小区间，即可确定a+1的大小区间，即可解题．
解答 解：画出草图，
∵0＜m＜$\frac{1}{2}$，∴△=4-8m＞0，
∵对称轴为x=$\frac{1}{2}$，x=0或1时，y=m＞0，
∴当y＜0时，0＜a＜1，
∴1＜a+1＜2，
∵当x=1时，y=2-2+m=m，
当x=2时，y=8-4+m=m+4，
∴当x=a+1时，函数值y的取值范围为m＜y＜m+4，
故选 C．
点评 本题考查了抛物线上点的特性，考查了抛物线开口向上时，对称轴右侧点依次增大的特性，本题中确定a的取值范围是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
已知，（如图）AD⊥BC垂足为D，EF⊥BC垂足为F，若∠1=∠2，问GD与AC平行吗？为什么？
如图，菱形AB1C1D1的边长为1，∠B1=60°；作AD2⊥B1C1于点D2，以AD2为一边，做第二个菱形AB2C2D2，使∠B2=60°；作AD3⊥B2C2于点D3，以AD3为一边做第三个菱形AB3C3D3，使∠B3=60°…则AD2=$\frac{\sqrt{3}}{2}$，依此类推这样做的第n个菱形ABnCnDn的边ADn的长是（$\frac{\sqrt{3}}{2}$）n-1．
如图所示，在平行四边形ABCD中，对角线AC，BD相交于点O，若BD与AC的和为23，AB：AD=1：2，△COD的周长为15，求BC的长．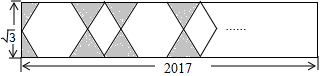
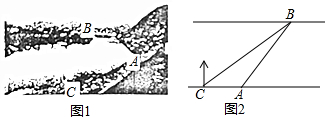如图1，某社会实践活动小组实地测量两岸互相平行的一段河的宽度，在河的南岸边点A处，测得河的北岸边点B在其北偏东45°方向，然后向西走50m到达C点，测得点B在点C的北偏东60°方向，如图2，求出这段河的宽（结果精确到1m，备用数据$\sqrt{2}$≈1.41，$\sqrt{3}$≈1.73）．
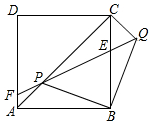边长为2$\sqrt{2}$的正方形ABCD中，P是对角线AC上的一个动点（点P与A、C不重合），连接BP，将BP绕点B顺时针旋转90°到BQ，连接QP，QP与BC交于点E，QP延长线与AD（或AD延长线）交于点F．