Question

15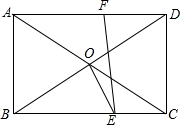．如图，矩形ABCD的两条对角线AC，BD相交于点O，夹角为60°，点E，F分别在BC，AD上，四边形ABEF是正方形，连接OE，则∠BOE=75°．

Answer 1

分析 由矩形ABCD的两条对角线AC，BD相交于点O，夹角为60°，可得△AOB是等边三角形，又由四边形ABEF是正方形，可得△OBE是等腰三角形，继而求得答案．

解答 解：∵四边形ABCD是矩形，
∴OA=OB，∠ABC=90°，
∵∠AOB=60°，
∴△AOB是等边三角形，
∴∠ABO=60°，OB=AB，
∴∠OBE=30°，
∵四边形ABEF是正方形，
∴AB=BE，
∴OB=BE，
∴∠BOE=∠BEO=75°．
故答案为：75°．

点评 此题考查了正方形的性质、矩形的性质以及等边三角形的判定与性质．注意证得△AOB是等边三角形是解此题的关键．