题目内容
9. 如图,E,F,G,H分别是边BD、BC、AC、AD的中点,且AB=CD=6,现有下列结论:①EG⊥FH;②四边形EFGH是矩形;③HF平分∠EHG;④四边形EFGH的周长是12.其中正确的是①③④.(把所有正确结论的序号都选上)
如图,E,F,G,H分别是边BD、BC、AC、AD的中点,且AB=CD=6,现有下列结论:①EG⊥FH;②四边形EFGH是矩形;③HF平分∠EHG;④四边形EFGH的周长是12.其中正确的是①③④.(把所有正确结论的序号都选上)
分析 根据三角形的中位线平行于第三边并且等于第三边的一半与AB=CD可得四边形EFGH是菱形,然后根据菱形的对角线互相垂直平分,并且平分每一组对角的性质对各小题进行判断.
解答 解:∵E、F、G、H分别是BD、BC、AC、AD的中点,
∴EF=$\frac{1}{2}$CD,FG=$\frac{1}{2}$AB,GH=$\frac{1}{2}$CD,HE=$\frac{1}{2}$AB,
∵AB=CD,
∴EF=FG=GH=HE,
∴四边形EFGH是菱形,
∴①EG⊥FH,正确;
②四边形EFGH是矩形,错误;
③HF平分∠EHG,正确;
④四边形EFGH的周长=$\frac{1}{2}$(CD+AB+CD+AB)=12,正确.
综上所述,①③④共3个正确.
故答案是:①③④.
点评 本题考查了三角形中位线定理与菱形的判定与菱形的性质,根据三角形的中位线定理与AB=CD判定四边形EFGH是菱形是解答本题的关键.

练习册系列答案
相关题目
10. 把一个边长为1的正方形如图所示放在数轴上,以正方形的对角线为半径画弧交数轴于点A,则点A对应的数是( )
把一个边长为1的正方形如图所示放在数轴上,以正方形的对角线为半径画弧交数轴于点A,则点A对应的数是( )
 把一个边长为1的正方形如图所示放在数轴上,以正方形的对角线为半径画弧交数轴于点A,则点A对应的数是( )
把一个边长为1的正方形如图所示放在数轴上,以正方形的对角线为半径画弧交数轴于点A,则点A对应的数是( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
17.计算5-2正确的是( )
| A. | -10 | B. | $-\frac{1}{25}$ | C. | $\frac{1}{25}$ | D. | 25 |
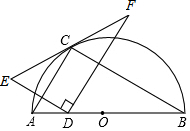 如图,点C在以AB为直径的半圆上,AB=4$\sqrt{5}$,AC=4,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE,DF交EC的延长线于点F,当点D从点A运动到点B时,线段EF扫过的面积是32.
如图,点C在以AB为直径的半圆上,AB=4$\sqrt{5}$,AC=4,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE,DF交EC的延长线于点F,当点D从点A运动到点B时,线段EF扫过的面积是32.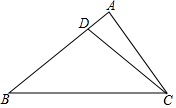 如图,在△ABC中,AB=8cm,AC=6cm,BC=10cm,点D在AB上,且BD=CD,求△BDC的面积.
如图,在△ABC中,AB=8cm,AC=6cm,BC=10cm,点D在AB上,且BD=CD,求△BDC的面积.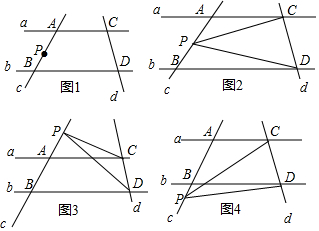
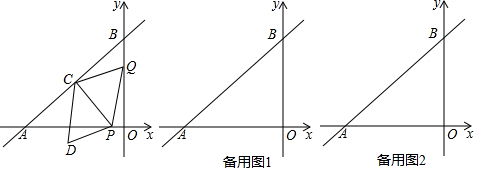
 如图,一次函数y1=x+b与一次函数y2=kx+4的图象交于点P(1,3),则关于x的不等式x+b≤kx+4的解集是x≤1.
如图,一次函数y1=x+b与一次函数y2=kx+4的图象交于点P(1,3),则关于x的不等式x+b≤kx+4的解集是x≤1.