题目内容
 如图,在⊙O中,AB是弦,OC、OD是半径,且分别与AB交于E、F,若
如图,在⊙O中,AB是弦,OC、OD是半径,且分别与AB交于E、F,若 |
| AC |
 |
| BD |
考点:圆心角、弧、弦的关系,全等三角形的判定与性质
专题:证明题
分析:连接OA,OB.由OA=OB得出∠OAE=∠OBF,由弧AC=弧BD得出∠AOC=∠BOD,利用ASA证明△OAE≌△OBF,由此得出AE=BF.
解答: 证明:如图,连接OA,OB.
证明:如图,连接OA,OB.
∵OA=OB,
∴∠OAE=∠OBF,
又∵弧AC=弧BD,
∴∠AOC=∠BOD.
在△OAE与△OBF中,
,
∴△OAE≌△OBF(ASA),
∴AE=BF.
 证明:如图,连接OA,OB.
证明:如图,连接OA,OB.∵OA=OB,
∴∠OAE=∠OBF,
又∵弧AC=弧BD,
∴∠AOC=∠BOD.
在△OAE与△OBF中,
|
∴△OAE≌△OBF(ASA),
∴AE=BF.
点评:本题考查了圆心角、弧、弦关系定理的推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.同时考查了全等三角形的判定与性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知∠AOB=α,过点O任作一射线OC,OM平分∠AOC,ON平分∠BOC,
已知∠AOB=α,过点O任作一射线OC,OM平分∠AOC,ON平分∠BOC,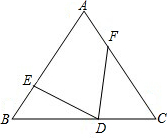 如图所示,△ABC是等边三角形,点D,E,F分别是边BC,AB,AC边上的点,且BE=CD,∠EDF=60°,求证:ED=FD.
如图所示,△ABC是等边三角形,点D,E,F分别是边BC,AB,AC边上的点,且BE=CD,∠EDF=60°,求证:ED=FD. 如图,C是线段AB上一点,△ACD和△BCE都是等边三角形,AE交CD于点M,BD交CE于点N,交AE于点O,求证:
如图,C是线段AB上一点,△ACD和△BCE都是等边三角形,AE交CD于点M,BD交CE于点N,交AE于点O,求证: