题目内容
16.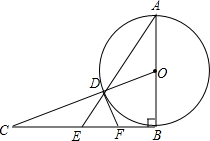 如图,AB=BC,∠ABC=90°,以AB为直径的⊙O交OC于点D,AD的延长线交BC于点E,点F为BE的中点.
如图,AB=BC,∠ABC=90°,以AB为直径的⊙O交OC于点D,AD的延长线交BC于点E,点F为BE的中点.(1)求证:DF为⊙O的切线;
(2)求证:CD2=CE•CB;
(3)若CE=4,求DF的长.
分析 (1)先连接BD,利用圆周角定理求得BD⊥AE,然后根据三角形斜边的性质求得DF=BF,然后根据等腰三角形的性质即可证得∠ODF=90°;
(2)根据直角三角形两锐角互余和等腰三角形的性质求得∠CDB=∠CED,进而得出△CDE∽△CBD,再根据相似三角形的性质即可得出答案.
(3)先求得△CDF∽△CBO,再根据相似三角形的性质求得2DF=CD,再结合(2)求得的结论即可求得DF的长.
解答 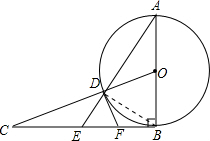 解:(1)连接BD,
解:(1)连接BD,
∵AB为直径,
∴∠ADB=90°,
∴∠EDB=90°,
∵点F为BE的中点,
∴DF=BF,
∴∠BDF=∠DBF,
∴OD=OB,
∴∠ODB=∠OBD,
∴∠ODB+∠BDF=∠OBD+∠DBF,
即∠ODF=∠OBF,
∵∠ABC=90°,
∴∠ODF=90°,
∴DF为⊙O的切线;
(2)∵AB为直径,
∴∠ADB=90°,
∴∠OBD+∠A=90°,
∵∠ABC=90°,
∴∠DEB+∠A=90°,
∴∠DEB=∠OBD,
∴∠ODB=∠OBD,
∴∠ODB=∠DEB,
∴∠CDB=∠CED,
∵∠DCB=∠ECD,
∴△CDE∽△CBD,
∴$\frac{CE}{CD}$=$\frac{CD}{CB}$,
∴CD2=CE•CB;
(3)∵∠CDF=∠CBO=90°,
∠DCF=∠OCB,
∴△CDF∽△CBO,
∴$\frac{DF}{BO}$=$\frac{CD}{BC}$,
∴$\frac{DF}{CD}$=$\frac{BO}{CB}$,
∵AB=BC,
∴$\frac{DF}{CD}$=$\frac{BO}{CB}$=$\frac{1}{2}$,
∴2DF=CD,
∵CD2=CE•CB,BE=2DF,
∴(2DF)2=CE(CE+2DF),
∴4DF2=4(4+2DF),
解得DF=$\sqrt{5}$-1.
点评 此题主要考查了圆的切线性质与判定、圆周角定理性质及三角形相似的判定等知识,熟练根据相似三角形的性质得出对应边之间关系是解题关键.

 如图,AB是⊙O的直径,AF是⊙O的切线,弦CD⊥AB于E,CF∥DA,DE=2$\sqrt{3}$,AO-OE=2,证明四边形AFCD是菱形,并求点O到FC的距离.
如图,AB是⊙O的直径,AF是⊙O的切线,弦CD⊥AB于E,CF∥DA,DE=2$\sqrt{3}$,AO-OE=2,证明四边形AFCD是菱形,并求点O到FC的距离.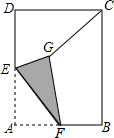 如图,在矩形ABCD中,AD=6,CD=4,AD的中点为E,点F是AB边上一点(不与A、B重合),连接EF,把∠A沿EF折叠,使点A落在点G处,连接CG.则线段CG的取值范围是$\frac{2}{5}$$\sqrt{37}$<CG<2$\sqrt{13}$.
如图,在矩形ABCD中,AD=6,CD=4,AD的中点为E,点F是AB边上一点(不与A、B重合),连接EF,把∠A沿EF折叠,使点A落在点G处,连接CG.则线段CG的取值范围是$\frac{2}{5}$$\sqrt{37}$<CG<2$\sqrt{13}$. 已知,如图:四边形ABCD,点E在线段AD的延长线上,连接BE,AB∥CD,∠1=∠2.求证:∠A=∠C.
已知,如图:四边形ABCD,点E在线段AD的延长线上,连接BE,AB∥CD,∠1=∠2.求证:∠A=∠C.