题目内容
17.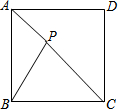 如图,P为正方形内一点,若PA:PB:PC=1:2:3,则∠APB的度数是( )
如图,P为正方形内一点,若PA:PB:PC=1:2:3,则∠APB的度数是( )| A. | 120° | B. | 135° | C. | 145° | D. | 150° |
分析 利用PA:PB:PC=1:2:3可设PA=a,PB=2a,PC=3a,再根据正方形的性质得AB=BC,∠ABC=90°,则可把△ABP绕点B顺时针旋转90°得到△BCQ,如图,根据旋转的性质得∠PBQ=90°,∠BQC=∠BPA,BP=BQ=2a,CQ=AP=a,则可判断△PBQ为等腰直角三角形,得到PQ=$\sqrt{2}$PB=2$\sqrt{2}$a,∠PQB=45°,然后在△PCQ中根据勾股定理的逆定理可证明△PCQ为直角三角形,∠PQC=90°,于是∠BQC=∠PQB+∠PQC=135°,所以∠APB=135°.
解答 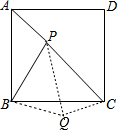 解:由PA:PB:PC=1:2:3,可设PA=a,PB=2a,PC=3a,
解:由PA:PB:PC=1:2:3,可设PA=a,PB=2a,PC=3a,
∵四边形ABCD为正方形,
∴AB=BC,∠ABC=90°,
把△ABP绕点B顺时针旋转90°可得到△BCQ,如图,
∴∠PBQ=90°,∠BQC=∠BPA,BP=BQ=2a,CQ=AP=a,
∴△PBQ为等腰直角三角形,
∴PQ=$\sqrt{2}$PB=2$\sqrt{2}$a,∠PQB=45°,
在△PCQ中,∵PQ=2$\sqrt{2}$a,CQ=a,PC=3a,
∴PQ2+CQ2=PC2,
∴△PCQ为直角三角形,∠PQC=90°,
∴∠BQC=∠PQB+∠PQC=45°+90°=135°,
∴∠APB=135°.
故选B.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了勾股定理的逆定理和正方形的性质.

练习册系列答案
相关题目
2.已知mn<0,$\frac{1}{m^2}+\frac{1}{n^2}$=1,化简m$\sqrt{1-\frac{1}{m^2}}-n\sqrt{1-\frac{1}{n^2}}$以后得到的结果是( )
| A. | mn或-mn | B. | -mn | C. | mn | D. | 2 |
7.下列计算错误的是( )
| A. | (-4xy2)3=-12x3y6 | B. | 2a3+a3=3a3 | C. | m4•m2=m6 | D. | 2-2=$\frac{1}{4}$ |
 已知,如图:四边形ABCD,点E在线段AD的延长线上,连接BE,AB∥CD,∠1=∠2.求证:∠A=∠C.
已知,如图:四边形ABCD,点E在线段AD的延长线上,连接BE,AB∥CD,∠1=∠2.求证:∠A=∠C. 求阴影部分的面积.
求阴影部分的面积.