Question

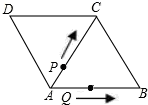如图，菱形ABCD的边长为12cm，∠B=60°，从初始时刻开始，点P、Q同时从A点出发，点P以2cm/秒的速度沿A→C→B的方向运动，点Q以4cm/秒的速度沿A→B→C→D的方向运动，当Q点运动点D点时，P、Q两点同时停止运动．设P、Q运动的时间为x秒时，解答下列问题：
（1）点P、Q从出发到相遇所用时间是

 

秒；
（2）点P、Q从开始运动到停止的过程中，当△APQ是等边三角形时，请求此时x的值是多少秒？

Answer 1

考点：菱形的性质,等边三角形的性质

专题：动点型

分析：（1）菱形ABCD的边长为12厘米，∠B=60°，则易证△ABC是等边三角形，边长是12厘米．点P、Q从出发到相遇，即两人所走的路程的和是36cm．设从出发到相遇所用的时间是x秒．列方程就可以求出时间．
（2）当P在AC上，Q在AB上时，AP≠AQ，则一定不是等边三角形，当△APQ是等边三角形时，Q一定在边CD上，P一定在边CB上，若△APQ是等边三角形，则CP=DQ，根据这个相等关系，就可以得到一个关于x的方程，就可以得到x的值．

解答：解：（1）∵四边形ABCD是菱形，
∴AB=BC=12cm，
又∵∠B=60°，
∴△ABC是等边三角形，
设点P，Q从出发到相遇所用的时间是x秒．
根据题意得：2x+4x=12×3，
解得x=6．
即点P、Q从出发到相遇所用时间是6秒；
故答案为：6；

（2）若△APQ是等边三角形，
此时点P在BC上，点Q在CD上，且△ADQ≌△ACP，
则CP=DQ，
即2x-12=36-4x，
解得x=8．

点评：此题考查了菱形的性质以及等边三角形的判定与性质．此题难度适中，注意掌握数形结合思想与方程思想的应用．