题目内容
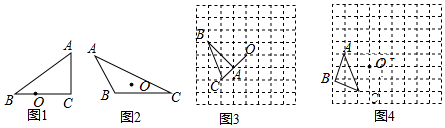
18. 在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1.点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B按逆时针方向旋转过程中,点P的对应点是点P1,则线段EP1长度的最大值与最小值的差为9-$\frac{5\sqrt{2}}{2}$.
在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1.点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B按逆时针方向旋转过程中,点P的对应点是点P1,则线段EP1长度的最大值与最小值的差为9-$\frac{5\sqrt{2}}{2}$.
分析 过点B作BD⊥AC,D为垂足,在Rt△BCD中,根据BD=BC×sin45°求出BD的长.①当P在AC上运动至垂足点D,△ABC绕点B旋转,点P的对应点P1在线段AB上时,EP1最小;②当P在AC上运动至点C,△ABC绕点B旋转,点P的对应点P1在线段AB的延长线上时,EP1最大,据此求解可得.
解答 解:如图,过点B作BD⊥AC,D为垂足,
∵△ABC为锐角三角形,
∴点D在线段AC上,
在Rt△BCD中,BD=BC×sin45°=$\frac{5\sqrt{2}}{2}$.
①当P在AC上运动至垂足点D,△ABC绕点B旋转,点P的对应点P1在线段AB上时,EP1最小,最小值为$\frac{5\sqrt{2}}{2}$-2
②当P在AC上运动至点C,△ABC绕点B旋转,点P的对应点P1在线段AB的延长线上时,EP1最大,最大值为2+5=7,
∴线段EP1长度的最大值与最小值的差为7-$\frac{5\sqrt{2}}{2}$+2=9-$\frac{5\sqrt{2}}{2}$,
故答案为:9-$\frac{5\sqrt{2}}{2}$.
点评 本题主要考查旋转变换、解直角三角形的应用,根据题意得出点P的对应点P1在线段AB上时EP1最小、点P的对应点P1在线段AB的延长线上时EP1最大是解题的关键.

练习册系列答案
相关题目
6.已知某圆锥的底面圆的半径r=2cm,将圆锥侧面展开得到一个圆心角θ=120°的扇形,则该圆锥的母线长l为( )
| A. | 3cm | B. | 4cm | C. | 5cm | D. | 6cm |
10.已知⊙O的半径为$\sqrt{3}$,点P到圆心O的距离为2,则点P与⊙O的位置关系是( )
| A. | 点P在⊙O外 | B. | 点P在⊙O上 | C. | 点P在⊙O内 | D. | 无法确定 |
7. 如图是用相同的正方形砖铺成的地面,一宝物藏在其中某一块砖的下面,则宝物在白色区域的概率是( )
如图是用相同的正方形砖铺成的地面,一宝物藏在其中某一块砖的下面,则宝物在白色区域的概率是( )
 如图是用相同的正方形砖铺成的地面,一宝物藏在其中某一块砖的下面,则宝物在白色区域的概率是( )
如图是用相同的正方形砖铺成的地面,一宝物藏在其中某一块砖的下面,则宝物在白色区域的概率是( )| A. | $\frac{2}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{7}{15}$ | D. | $\frac{8}{15}$ |
8.已知△ABC≌△DEF,若△ABC的周长为20,AB=5,BC=6,则DF的长度为( )
| A. | 5 | B. | 6 | C. | 9 | D. | 11 |
 如图,三个全等的小矩形沿“橫-竖-橫”排列在一个大矩形中,若这个大矩形的周长为2016cm,则一个小矩形的周长等于672cm.
如图,三个全等的小矩形沿“橫-竖-橫”排列在一个大矩形中,若这个大矩形的周长为2016cm,则一个小矩形的周长等于672cm.