题目内容
12.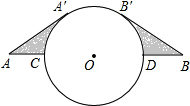 如图,相距40km的两个城镇A,B之间有一个圆形湖泊,它的圆心落在AB连线的中点O,半径为10km.现要修建一条连接两城镇的公路.经过论证,认为AA′+$\widehat{A′B′}$+BB′为最短路线(其中AA′,BB′都与⊙O相切).
如图,相距40km的两个城镇A,B之间有一个圆形湖泊,它的圆心落在AB连线的中点O,半径为10km.现要修建一条连接两城镇的公路.经过论证,认为AA′+$\widehat{A′B′}$+BB′为最短路线(其中AA′,BB′都与⊙O相切).(1)你能计算出这段公路的长度吗?(结果精确到0.1km)
(2)阴影部分的面积是多少?(结果精确到1km2)
分析 (1)连结OA′、OB′,如图,根据切线的性质得OA′⊥AA′,OB′⊥BB′,再计算出OA=OB=$\frac{1}{2}$AB=20,在Rt△OAA′中,利用正弦的定义可求出∠A=30°,则∠AOA′=60°,AA′=$\sqrt{3}$OA′=10$\sqrt{3}$,同理可得∠BOB′=60°,BB′=10$\sqrt{3}$,于是∠A′OB′=60°,接着根据弧长公式计算出弧A′B′的长度,然后求AA′+$\widehat{A′B′}$+BB′的值即可;
(2)用△AA′O与△BB′O的面积减去扇形A′OC和扇形B′OD的面积即可.
解答 解:(1)连结OA′、OB′,如图,
∵AA′,BB′都与⊙O相切,
∴OA′⊥AA′,OB′⊥BB′,
∵点O为AB的中点,
∴OA=OB=$\frac{1}{2}$AB=20,
而OA′=OB′=10,
在Rt△OAA′中,∵sin∠A=$\frac{OA′}{OA}$=$\frac{10}{20}$=$\frac{1}{2}$,
∴∠A=30°,
∴∠AOA′=60°,AA′=$\sqrt{3}$OA′=10$\sqrt{3}$,
同理可得∠BOB′=60°,BB′=10$\sqrt{3}$,
∴∠A′OB′=60°,
∴弧A′B′的长度=$\frac{60•π•10}{180}$=$\frac{10}{3}$π,
∴这段公路的长度=10$\sqrt{3}$+$\frac{10}{3}$π+10$\sqrt{3}$≈45.1(km);
(2)S△AA′O=$\frac{1}{2}AA′•AO$•sin∠A=$\frac{1}{2}$×10$\sqrt{3}$×20×$\frac{1}{2}$=50$\sqrt{3}$,
S△B′OB=S△AA′O=50$\sqrt{3}$,
S扇形A′OC=$\frac{n{πr}^{2}}{360°}$=$\frac{60°π{•10}^{2}}{360°}$=$\frac{50}{3}π$,同理可得,S扇形B′OB=$\frac{50}{3}π$,
所以S阴影=S△AA′O+S△B′OB-S扇形A′OC -S扇形B′OB=2×50$\sqrt{3}$-2×$\frac{50}{3}π$=100$\sqrt{3}$$-\frac{100}{3}$π=69(km2).
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了弧长公式,扇形的面积公式,作出适当的辅助线是解答此题的关键.

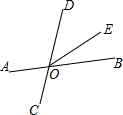 已知如图,直线AB、CD相交于点O,∠AOC=60°,OE把∠BOD分成两部分,且∠BOE:∠EOD=1:2,则∠AOE=( )
已知如图,直线AB、CD相交于点O,∠AOC=60°,OE把∠BOD分成两部分,且∠BOE:∠EOD=1:2,则∠AOE=( )| A. | 180° | B. | 160° | C. | 140° | D. | 120° |
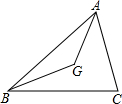 已知G点为△ABC的重心,S△ABG=1,求S△ABC=3.
已知G点为△ABC的重心,S△ABG=1,求S△ABC=3.