题目内容
17.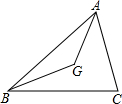 已知G点为△ABC的重心,S△ABG=1,求S△ABC=3.
已知G点为△ABC的重心,S△ABG=1,求S△ABC=3.
分析 首先延长AG交BC于点D,判断出点D是BC边的中点,即可判断出S△ABD=S△ACD=$\frac{1}{2}$S△ABC;然后根据三角形的面积和底的正比关系,求出△ABD的面积,即可求出S△ABC的值是多少.
解答 解:如图1,延长AG交BC于点D,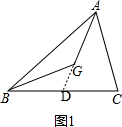 ,
,
∵G点为△ABC的重心,
∴点D是BC边的中点,
∴S△ABD=S△ACD=$\frac{1}{2}$S△ABC;
∵G点为△ABC的重心,
∴AG:GD=2:1,
∴AG=$\frac{2}{3}$AD,
∴S△ABG=$\frac{2}{3}$S△ABD,
∴S△ABD=1÷$\frac{2}{3}=\frac{3}{2}$,
∴S△ABC=2S△ABD=2×$\frac{3}{2}$=3.
故答案为:3.
点评 此题主要考查了三角形的重心的性质和应用,要熟练掌握,解答此题的关键是要明确:①重心到顶点的距离与重心到对边中点的距离之比为2:1.②重心和三角形3个顶点组成的3个三角形面积相等.③重心到三角形3个顶点距离的和最小.

练习册系列答案
相关题目
8.若x1,x2是方程x2-2x-2012=0的两个实根,则代数式x12+2x1•x2-2x1的值为( )
| A. | 0 | B. | -2012 | C. | 2012 | D. | 4024 |
6.下列调查中,适合采用全面调查的是( )
| A. | 了解集安市中学生的视力情况 | B. | 了解集安市中学生的课外阅读情况 | ||
| C. | 了解集安市百岁老人的健康情况 | D. | 了解集安市老年人参加晨练的情况 |
7.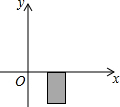 在一次科学探测活动中,探测人员发现一目标在如图所示的阴影区域内,则目标的坐标可能是( )
在一次科学探测活动中,探测人员发现一目标在如图所示的阴影区域内,则目标的坐标可能是( )
 在一次科学探测活动中,探测人员发现一目标在如图所示的阴影区域内,则目标的坐标可能是( )
在一次科学探测活动中,探测人员发现一目标在如图所示的阴影区域内,则目标的坐标可能是( )| A. | (-3,300) | B. | (7,-500) | C. | (9,600) | D. | (-2,-800) |
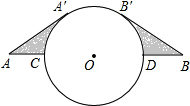 如图,相距40km的两个城镇A,B之间有一个圆形湖泊,它的圆心落在AB连线的中点O,半径为10km.现要修建一条连接两城镇的公路.经过论证,认为AA′+$\widehat{A′B′}$+BB′为最短路线(其中AA′,BB′都与⊙O相切).
如图,相距40km的两个城镇A,B之间有一个圆形湖泊,它的圆心落在AB连线的中点O,半径为10km.现要修建一条连接两城镇的公路.经过论证,认为AA′+$\widehat{A′B′}$+BB′为最短路线(其中AA′,BB′都与⊙O相切).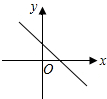

 如图,平面直角坐标系中,三角形ABC的顶点都在网格点上,平移三角形ABC,使点B与坐标原点O重合.请写出图中点A,B,C的坐标并画出平移后的三角形A1OC1.
如图,平面直角坐标系中,三角形ABC的顶点都在网格点上,平移三角形ABC,使点B与坐标原点O重合.请写出图中点A,B,C的坐标并画出平移后的三角形A1OC1.