题目内容
4.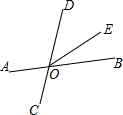 已知如图,直线AB、CD相交于点O,∠AOC=60°,OE把∠BOD分成两部分,且∠BOE:∠EOD=1:2,则∠AOE=( )
已知如图,直线AB、CD相交于点O,∠AOC=60°,OE把∠BOD分成两部分,且∠BOE:∠EOD=1:2,则∠AOE=( )| A. | 180° | B. | 160° | C. | 140° | D. | 120° |
分析 根据对顶角相等求出∠BOD的度数,再根据∠BOE:∠EOD=1:2求出∠BOE的度数,然后利用互为邻补角的两个角的和等于180°即可求出∠AOE的度数.
解答 解:∵∠AOC=60°,
∴∠BOD=∠AOC=60°,
∵∠BOE:∠EOD=1:2,
∴∠BOE=$\frac{1}{3}$×60°=20°,
∴∠AOE=180°-20°=160°.
故选:B.
点评 本题考查了对顶角相等的性质,邻补角的定义,熟记性质并准确识图是解题的关键.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
19.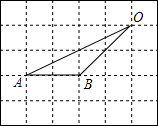 如图,在网格中,小正方形的边长均为1,点A、B、O都在格点上,则∠AOB的正弦值是( )
如图,在网格中,小正方形的边长均为1,点A、B、O都在格点上,则∠AOB的正弦值是( )
 如图,在网格中,小正方形的边长均为1,点A、B、O都在格点上,则∠AOB的正弦值是( )
如图,在网格中,小正方形的边长均为1,点A、B、O都在格点上,则∠AOB的正弦值是( )| A. | $\frac{10\sqrt{10}}{3}$ | B. | $\frac{\sqrt{10}}{10}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
16.一元二次方程$\sqrt{2}{x}^{2}$-2$\sqrt{3}$x+$\sqrt{5}$=0的根的情况是( )
| A. | 方程没有实数根 | B. | 方程有两个相等的实数根 | ||
| C. | 方程有两个不相等的实数根 | D. | 无法判断方程实数根情况 |
13.三角形的三边长分别是3,1-2a,8.则数a的取值范围是( )
| A. | -5<a<-2 | B. | -5<a<2 | C. | 5<a<11 | D. | 0<a<2 |
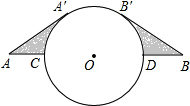 如图,相距40km的两个城镇A,B之间有一个圆形湖泊,它的圆心落在AB连线的中点O,半径为10km.现要修建一条连接两城镇的公路.经过论证,认为AA′+$\widehat{A′B′}$+BB′为最短路线(其中AA′,BB′都与⊙O相切).
如图,相距40km的两个城镇A,B之间有一个圆形湖泊,它的圆心落在AB连线的中点O,半径为10km.现要修建一条连接两城镇的公路.经过论证,认为AA′+$\widehat{A′B′}$+BB′为最短路线(其中AA′,BB′都与⊙O相切). 如图,平面直角坐标系中,三角形ABC的顶点都在网格点上,平移三角形ABC,使点B与坐标原点O重合.请写出图中点A,B,C的坐标并画出平移后的三角形A1OC1.
如图,平面直角坐标系中,三角形ABC的顶点都在网格点上,平移三角形ABC,使点B与坐标原点O重合.请写出图中点A,B,C的坐标并画出平移后的三角形A1OC1.