题目内容
3.一个多边形除去一个内角后,其余内角的和为1680°,它是12边形.分析 根据多边形的内角和公式(n-2)•180°可知多边形的内角和是180°的倍数,然后用1660°÷180°所得商的整数部分加1就是(n-2)的值.
解答 解:设多边形的边数是n,则(n-2)•180°=1680°,
解得n=11…60,
∵除去了一个内角,
∴边数是11+1=12,
故这个多边形的边数为12.
故答案为:12.
点评 本题考查了多边形的内角和公式,根据公式利用多边形的内角和是180°的倍数是解题的关键.

练习册系列答案
相关题目
8.若x1,x2是方程x2-2x-2012=0的两个实根,则代数式x12+2x1•x2-2x1的值为( )
| A. | 0 | B. | -2012 | C. | 2012 | D. | 4024 |
13.三角形的三边长分别是3,1-2a,8.则数a的取值范围是( )
| A. | -5<a<-2 | B. | -5<a<2 | C. | 5<a<11 | D. | 0<a<2 |
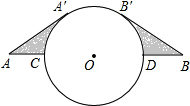 如图,相距40km的两个城镇A,B之间有一个圆形湖泊,它的圆心落在AB连线的中点O,半径为10km.现要修建一条连接两城镇的公路.经过论证,认为AA′+$\widehat{A′B′}$+BB′为最短路线(其中AA′,BB′都与⊙O相切).
如图,相距40km的两个城镇A,B之间有一个圆形湖泊,它的圆心落在AB连线的中点O,半径为10km.现要修建一条连接两城镇的公路.经过论证,认为AA′+$\widehat{A′B′}$+BB′为最短路线(其中AA′,BB′都与⊙O相切).