题目内容
9. 如图,在菱形ABCD中,点A在x轴上,点B的坐标为(8,2),点D的坐标为(0,2),则点C的坐标为(4,4).
如图,在菱形ABCD中,点A在x轴上,点B的坐标为(8,2),点D的坐标为(0,2),则点C的坐标为(4,4).
分析 连接AC、BD交于点E,由菱形的性质得出AC⊥BD,AE=CE=$\frac{1}{2}$AC,BE=DE=$\frac{1}{2}$BD,由点B的坐标和点D的坐标得出OD=2,求出DE=4,AC=4,即可得出点C的坐标.
解答 解:连接AC、BD交于点E,如图所示: ∵四边形ABCD是菱形,
∵四边形ABCD是菱形,
∴AC⊥BD,AE=CE=$\frac{1}{2}$AC,BE=DE=$\frac{1}{2}$BD,
∵点B的坐标为(8,2),点D的坐标为(0,2),
∴OD=2,BD=8,
∴AE=OD=2,DE=4,
∴AC=4,
∴点C的坐标为:(4,4);
故答案为:(4,4).
点评 本题考查了菱形的性质、坐标与图形性质;熟练掌握菱形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.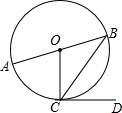 如图,在⊙O中,AB为直径,BC为弦,CD为切线,连接OC.若∠BCD=50°,则∠AOC的度数为( )
如图,在⊙O中,AB为直径,BC为弦,CD为切线,连接OC.若∠BCD=50°,则∠AOC的度数为( )
 如图,在⊙O中,AB为直径,BC为弦,CD为切线,连接OC.若∠BCD=50°,则∠AOC的度数为( )
如图,在⊙O中,AB为直径,BC为弦,CD为切线,连接OC.若∠BCD=50°,则∠AOC的度数为( )| A. | 40° | B. | 50° | C. | 80° | D. | 100° |
1.下列计算正确的是( )
| A. | x3+x=x4 | B. | x2•x3=x5 | C. | (x2)3=x5 | D. | x9÷x3=x3 |
18. 如图,直线a∥b,∠1=108°,则∠2的度数是( )
如图,直线a∥b,∠1=108°,则∠2的度数是( )
 如图,直线a∥b,∠1=108°,则∠2的度数是( )
如图,直线a∥b,∠1=108°,则∠2的度数是( )| A. | 72° | B. | 82° | C. | 92° | D. | 108° |
 如图,AB是⊙O的直径,AC是⊙O的弦,过点B作⊙O的切线DE,与AC的延长线交于点D,作AE⊥AC交DE于点E.
如图,AB是⊙O的直径,AC是⊙O的弦,过点B作⊙O的切线DE,与AC的延长线交于点D,作AE⊥AC交DE于点E. 如图,CE是△ABC外角∠ACD的平分线,AF∥CD交CE于点F,FG∥AC交CD于点G.求证:四边形ACGF是菱形.
如图,CE是△ABC外角∠ACD的平分线,AF∥CD交CE于点F,FG∥AC交CD于点G.求证:四边形ACGF是菱形.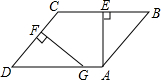 如图,在?ABCD中,AE⊥BC,交边BC于点E,点F为边CD上一点,且DF=BE.过点F作FG⊥CD,交边AD于点G.求证:DG=DC.
如图,在?ABCD中,AE⊥BC,交边BC于点E,点F为边CD上一点,且DF=BE.过点F作FG⊥CD,交边AD于点G.求证:DG=DC.