题目内容
14.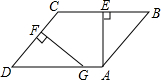 如图,在?ABCD中,AE⊥BC,交边BC于点E,点F为边CD上一点,且DF=BE.过点F作FG⊥CD,交边AD于点G.求证:DG=DC.
如图,在?ABCD中,AE⊥BC,交边BC于点E,点F为边CD上一点,且DF=BE.过点F作FG⊥CD,交边AD于点G.求证:DG=DC.
分析 先根据平行四边形的性质得到∠B=∠D,AB=CD,再利用垂直的定义得∠AEB=∠GFD=90°,于是可根据“ASA”判定△AEB≌△GFD,根据全等的性质得AB=DC,所以有DG=DC.
解答 证明:∵四边形ABCD为平行四边形,
∴∠B=∠D,AB=CD,
∵AE⊥BC,FG⊥CD,
∴∠AEB=∠GFD=90°,
在△AEB和△GFD中,
$\left\{\begin{array}{l}{∠B=∠D}\\{BE=DF}\\{∠AEB=∠GFD}\end{array}\right.$,
∴△AEB≌△GFD,
∴AB=DG,
∴DG=DC.
点评 本题考查了全等三角形的判定与性质:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.也考查了平行四边形的性质.

练习册系列答案
相关题目
5.方程x2-2x+3=0的根的情况是( )
| A. | 有两个相等的实数根 | B. | 只有一个实数根 | ||
| C. | 没有实数根 | D. | 有两个不相等的实数根 |
2. 如图,有一个正方体纸巾盒,它的平面展开图是( )
如图,有一个正方体纸巾盒,它的平面展开图是( )
 如图,有一个正方体纸巾盒,它的平面展开图是( )
如图,有一个正方体纸巾盒,它的平面展开图是( )| A. |  | B. |  | C. |  | D. |  |
 如图,在菱形ABCD中,点A在x轴上,点B的坐标为(8,2),点D的坐标为(0,2),则点C的坐标为(4,4).
如图,在菱形ABCD中,点A在x轴上,点B的坐标为(8,2),点D的坐标为(0,2),则点C的坐标为(4,4).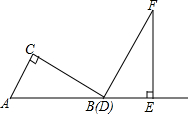 两个三角板ABC,DEF,按如图所示的位置摆放,点B与点D重合,边AB与边DE在同一条直线上(假设图形中所有的点,线都在同一平面内).其中,∠C=∠DEF=90°,∠ABC=∠F=30°,AC=DE=6cm.现固定三角板DEF,将三角板ABC沿射线DE方向平移,当点C落在边EF上时停止运动.设三角板平移的距离为x(cm),两个三角板重叠部分的面积为y(cm2).
两个三角板ABC,DEF,按如图所示的位置摆放,点B与点D重合,边AB与边DE在同一条直线上(假设图形中所有的点,线都在同一平面内).其中,∠C=∠DEF=90°,∠ABC=∠F=30°,AC=DE=6cm.现固定三角板DEF,将三角板ABC沿射线DE方向平移,当点C落在边EF上时停止运动.设三角板平移的距离为x(cm),两个三角板重叠部分的面积为y(cm2). 如图,已知直线m∥n,∠1=100°,则∠2的度数为80°.
如图,已知直线m∥n,∠1=100°,则∠2的度数为80°.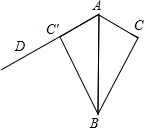 如图,△ABC的面积等于6,边AC=3,现将△ABC沿AB所在直线翻折,使点C落在直线AD上的C′处,点P在直线AD上,则线段BP的长不可能是( )
如图,△ABC的面积等于6,边AC=3,现将△ABC沿AB所在直线翻折,使点C落在直线AD上的C′处,点P在直线AD上,则线段BP的长不可能是( )