题目内容
4．
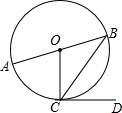如图，在⊙O中，AB为直径，BC为弦，CD为切线，连接OC．若∠BCD=50°，则∠AOC的度数为（ ）| A． | 40° | B． | 50° | C． | 80° | D． | 100° |
分析 根据切线的性质得出∠OCD=90°，进而得出∠OCB=40°，再利用圆心角等于圆周角的2倍解答即可．
解答 解：∵在⊙O中，AB为直径，BC为弦，CD为切线，
∴∠OCD=90°，
∵∠BCD=50°，
∴∠OCB=40°，
∴∠AOC=80°，
故选C．
点评 本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．推论：半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径，切线的性质：切线垂直于过切点的半径．
练习册系列答案
相关题目
14．
如图，将⊙O沿弦AB折叠，圆弧恰好经过圆心O，点P是优弧$\widehat{AMB}$上一点，则∠APB的度数为（ ）
如图，将⊙O沿弦AB折叠，圆弧恰好经过圆心O，点P是优弧$\widehat{AMB}$上一点，则∠APB的度数为（ ）| A． | 45° | B． | 30° | C． | 75° | D． | 60° |
如图，在平面直角坐标系中，点P在函数y=$\frac{6}{x}$（x＞0）的图象上．过点P分别作x轴、y轴的垂线，垂足分别为A、B，取线段OB的中点C，连结PC并延长交x轴于点D．则△APD的面积为6．
19．若等式0□1=-1成立，则□内的运算符号为（ ）
| A． | + | B． | - | C． | × | D． | ÷ |
如图，在菱形ABCD中，点A在x轴上，点B的坐标为（8，2），点D的坐标为（0，2），则点C的坐标为（4，4）．
要从甲、乙两名同学中选出一名，代表班级参加射击比赛，如图是两人最近10次射击训练成绩的折线统计图．