题目内容
15.若$\root{2n+1}{3m-2n}$与$\sqrt{3}$是同类最简二次根式,则求$\sqrt{mn}$的值.分析 由二次根式的根指数为2可知2n+1=2,然后依据同类二次根式的定义可知3m-2n=3,然后求得m、n的值,最后再求mn得算术平方根即可.
解答 解:由题意可知$\left\{\begin{array}{l}{2n+1=2}\\{3m-2n=3}\end{array}\right.$,
解得m=$\frac{4}{3}$,n=$\frac{1}{2}$,
即$\sqrt{mn}$=$\sqrt{\frac{4}{3}×\frac{1}{2}}$=$\frac{\sqrt{6}}{3}$.
点评 本题主要考查的是同类二次根式的定义,掌握同类二次根式的定义是解题的关键.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
6.下列各式中不是二次根式的是( )
| A. | $\sqrt{{x}^{2}+1}$ | B. | $\sqrt{4}$ | C. | $\sqrt{-3}$ | D. | $\sqrt{(a-b)^{2}}$ |
10.下列多项式乘法,能用平方差公式进行计算的是( )
| A. | (-a-b)(a-b) | B. | (2x+3y)(2x-3z) | C. | (x+y)(-x-y) | D. | (m-n)(n-m) |
5.计算(a2)4的结果是( )
| A. | a5 | B. | a6 | C. | a8 | D. | a9 |
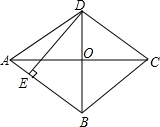 如图,菱形ABCD的两条对角线相交于点O,若AC=24,BD=10,过点D作DE⊥AB,垂足为E,则DE的长是$\frac{120}{13}$.
如图,菱形ABCD的两条对角线相交于点O,若AC=24,BD=10,过点D作DE⊥AB,垂足为E,则DE的长是$\frac{120}{13}$. 如图,在正方形ABCD的外侧,作等边△ADE,则∠EBD=30°.
如图,在正方形ABCD的外侧,作等边△ADE,则∠EBD=30°.