题目内容
15.在数轴上表示出-4,0,-$\frac{1}{2}$,$\frac{5}{2}$,-$\frac{2}{3}$;(2)将(1)中各数用“>”连接起来;
(3)将(1)中各数的相反数用“>”连接起来;
(4)将(1)中各数的绝对值用“<”连接起来.
分析 (1)把这五个数表示在数轴上,按右边的数总比左边的数大比较大小;
(2)分别计算这五个数的相反数,再将相反数依次标在数轴上来比较大小;
(3)分别计算这五个数的绝对值,再依次标在数轴上来比较大小.
解答  解:(1)如图1,则$\frac{5}{2}$>0>-$\frac{1}{2}$>-$\frac{2}{3}$>-4;
解:(1)如图1,则$\frac{5}{2}$>0>-$\frac{1}{2}$>-$\frac{2}{3}$>-4;
(2)如图2,-4的相反数是4,
0的相反数是0,
-$\frac{1}{2}$的相反数是$\frac{1}{2}$,
$\frac{5}{2}$的相反数是-$\frac{5}{2}$,
-$\frac{2}{3}$的相反数是$\frac{2}{3}$;
则4>$\frac{2}{3}$>$\frac{1}{2}$>0>-$\frac{5}{2}$;
(3)如图3,-4的绝对值是4,
0的绝对值是0,
-$\frac{1}{2}$的绝对值是$\frac{1}{2}$,
$\frac{5}{2}$的绝对值$\frac{5}{2}$,
-$\frac{2}{3}$的绝对值$\frac{2}{3}$;
则0<$\frac{1}{2}$<$\frac{2}{3}$$<\frac{5}{2}$<4.
点评 本题考查了有理数的大小比较和数轴,同时也考查了相反数和绝对值的定义,属于基础题,比较简单;有理数大小比较有两种方法:①根据正数大于0,0大于负数,正数大于负数,两个负数绝对值大的反而小;②利用数轴来比较大小,根据比较原则:数轴上的数右边的数总比左边的大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.在平面直角坐标系中,以点A(-1,0)为圆心,$\sqrt{2}$为半径画圆,若B为圆上任意一点,d为点B到x轴的距离,则下列关于d的说法中,正确的是( )
| A. | 有最大值2 | B. | 有最大值$\sqrt{2}$,但没有最小值 | ||
| C. | 没有最大值,但有最小值0 | D. | 既有最大值$\sqrt{2}$,又有最小值0 |
3.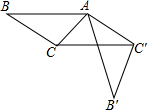 在△ABC中,∠CAB=26°,在同一平面内,将△ABC绕点A旋转α°到三角形AB'C'的位置使得CC'∥AB,则α=( )
在△ABC中,∠CAB=26°,在同一平面内,将△ABC绕点A旋转α°到三角形AB'C'的位置使得CC'∥AB,则α=( )
 在△ABC中,∠CAB=26°,在同一平面内,将△ABC绕点A旋转α°到三角形AB'C'的位置使得CC'∥AB,则α=( )
在△ABC中,∠CAB=26°,在同一平面内,将△ABC绕点A旋转α°到三角形AB'C'的位置使得CC'∥AB,则α=( )| A. | 138 | B. | 128 | C. | 118 | D. | 108 |
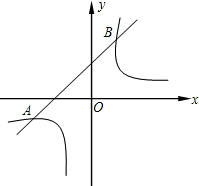 如图,已知双曲线y=$\frac{12}{x}$与直线y=x+1交于点A、B两点
如图,已知双曲线y=$\frac{12}{x}$与直线y=x+1交于点A、B两点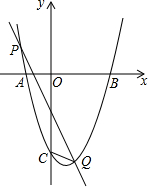 已知:抛物线y=x2+bx+c的对称轴x=1,与x轴交于A,B两点,且A(-1,0).与y轴交于点C,直线y=kx-1与抛物线交于P、Q两点且y轴平分△CPQ的面积.求k的值.
已知:抛物线y=x2+bx+c的对称轴x=1,与x轴交于A,B两点,且A(-1,0).与y轴交于点C,直线y=kx-1与抛物线交于P、Q两点且y轴平分△CPQ的面积.求k的值.