题目内容
10.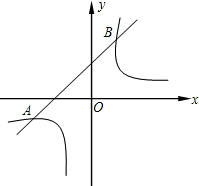 如图,已知双曲线y=$\frac{12}{x}$与直线y=x+1交于点A、B两点
如图,已知双曲线y=$\frac{12}{x}$与直线y=x+1交于点A、B两点(1)求点A、B两点的坐标;
(2)双曲线的图象上有三点M(x1,y1)、N(x2,y2)、P(x3,y3),且x1<x2<0<x3,则y1、y2、y3的大小关系是y2<y1<y3(用“<”号连接).
分析 (1)联立两函数解析式成方程组,解方程组即可得出交点A、B的坐标;
(2)根据12>0利用反比例函数的性质即可得出双曲线y=$\frac{12}{x}$在第三象限的图形单调递减,再结合x1<x2<0<x3,即可得出结论.
解答 解:(1)联立直线与双曲线解析式成方程组,得:$\left\{\begin{array}{l}{y=\frac{12}{x}}\\{y=x+1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=-4}\\{y=-3}\end{array}\right.$或$\left\{\begin{array}{l}{x=3}\\{y=4}\end{array}\right.$,
∴点A的坐标为(-4,-3),点B的坐标为(3,4).
(2)∵12>0,
∴双曲线y=$\frac{12}{x}$在第三象限的图形单调递减,
∵x1<x2<0,
∴y2<y1<0.
∵0<x3,
∴0<y3.
∴y2<y1<y3.
故答案为:y2<y1<y3.
点评 本题考查了反比例函数与一次函数的交点问题以及反比例的性质,解题的关键是:(1)联立两函数解析式成方程组,解方程组求出交点坐标;(2)根据反比例函数的性质找出其单调性.本题属于基础题,难度不大,解决该题型题目时,联立两函数的解析式成方程组,通过解方程组求出交点坐标是关键.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
20.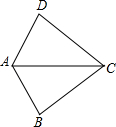 如图,已知∠DAC=∠BAC,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
如图,已知∠DAC=∠BAC,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
 如图,已知∠DAC=∠BAC,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
如图,已知∠DAC=∠BAC,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )| A. | AB=AD | B. | ∠BCA=∠DCA | C. | CB=CD | D. | ∠ADC=∠ABC |
18. 如图所示的几何体的左视图是( )
如图所示的几何体的左视图是( )
 如图所示的几何体的左视图是( )
如图所示的几何体的左视图是( )| A. |  | B. |  | C. |  | D. |  |
5.下列式子中不是整式的是( )
| A. | -23x | B. | a-2b=3 | C. | 12x+5y | D. | 0 |
19.某文具厂加工一种学生画图工具2500套,在加工了1000套后,采用了新技术,使每天的工作效率是原来的1.5倍,结果提前5天完成任务,若设该文具厂原来每天加工x套这种学生画图工具,则根据题意,可列方程( )
| A. | $\frac{2500}{x}$-$\frac{2500}{1.5x}$=5 | B. | $\frac{2500}{1.5x}$-$\frac{2500}{x}$=5 | ||
| C. | $\frac{1500}{1.5x}$=$\frac{1500}{x}$+5 | D. | $\frac{1000}{x}$+$\frac{1500}{1.5x}$=$\frac{2500}{x}$-5 |