题目内容
20.已知关于x的函数y=kx2+(2k-1)x-2(k为常数).(1)试说明:不论k取什么值,此函数图象一定经过(-2,0);
(2)在x>0时,若要使y随x的增大而减小,求k的取值范围;
(3)试问该函数是否存在最小值-3?若存在,请求出此时k的值;若不存在,请说明理由.
分析 (1)将x=-2代入计算,函数值为0即可.
(2)分两种情形讨论:①若k=0,此函数为一次函数y=-x-2,②若k≠0,根据二次函数的性质即可解决问题.
(3)分两种情形讨论:①若k=0,不存在,②k≠O,列出方程即可解决.
解答 解:(1)将x=-2代入,得y=k(-2)2+(2k-1)•(-2)-2=0,
故不论k取何值,此函数图象一定经过点(-2,0).
(2)①若k=0,此函数为一次函数y=-x-2,当x>0时,y随x的增大而减小,
∴k=0符合题意.
②若k≠0,此函数为二次函数,而图象一定经过(-2,0)、(0,-2)
∴要使当x>0时,y随x的增大而减小,开口向下,须满足k<0即可.
综上,k的取值范围是k≤0.
(3)若k=0,此函数为一次函数y=-x-2,
∵x的取值为全体实数,
∴y无最小值,
若k≠0,此函数为二次函数,若存在最小值为-3,
则$\frac{-8k-(2k-1)^{2}}{4k}$=-3,且k>0,
解得:k=$\frac{2±\sqrt{3}}{2}$ 符合题意,
∴当k=$\frac{2±\sqrt{3}}{2}$时,函数存在最小值-3.
点评 本题考查二次函数的最值问题、一次函数的有关知识,解题的关键是学会分类讨论,注意解题的严谨性,属于中考常考题型.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
10.下列运算正确的是( )
| A. | x3x2=x6 | B. | (-2x3)(-3x2)=6x5 | C. | (-2x)2=-4x2 | D. | x2+x2=2x4 |
11.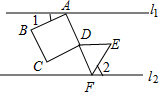 如图,直线l1∥l2,正方形ABCD的顶点A在l1上,顶点B、C、D在l1下方,等边三角形DEF的顶点F在上l2,顶点D、E在l2上方,且点A、D、F在同一直线上,若∠2=60°,则∠1的大小为( )
如图,直线l1∥l2,正方形ABCD的顶点A在l1上,顶点B、C、D在l1下方,等边三角形DEF的顶点F在上l2,顶点D、E在l2上方,且点A、D、F在同一直线上,若∠2=60°,则∠1的大小为( )
 如图,直线l1∥l2,正方形ABCD的顶点A在l1上,顶点B、C、D在l1下方,等边三角形DEF的顶点F在上l2,顶点D、E在l2上方,且点A、D、F在同一直线上,若∠2=60°,则∠1的大小为( )
如图,直线l1∥l2,正方形ABCD的顶点A在l1上,顶点B、C、D在l1下方,等边三角形DEF的顶点F在上l2,顶点D、E在l2上方,且点A、D、F在同一直线上,若∠2=60°,则∠1的大小为( )| A. | 30° | B. | 60° | C. | 45° | D. | 15° |
15.下列现象是平移的是( )
| A. | 钟摆的运动 | B. | 方向盘的转动 | C. | 汽车车轮的运动 | D. | 电梯的升降 |
9. 如图,直线a∥b,△ABC为等腰直角三角形,∠BAC=90°,则∠1的度数为( )
如图,直线a∥b,△ABC为等腰直角三角形,∠BAC=90°,则∠1的度数为( )
 如图,直线a∥b,△ABC为等腰直角三角形,∠BAC=90°,则∠1的度数为( )
如图,直线a∥b,△ABC为等腰直角三角形,∠BAC=90°,则∠1的度数为( )| A. | 90° | B. | 60° | C. | 45° | D. | 30° |
10. 如图,AB是⊙O的直径,点D、E是半圆的三等分点,AE、BD的延长线交于点C,若CE=2,则图中阴影部分的面积是( )
如图,AB是⊙O的直径,点D、E是半圆的三等分点,AE、BD的延长线交于点C,若CE=2,则图中阴影部分的面积是( )
 如图,AB是⊙O的直径,点D、E是半圆的三等分点,AE、BD的延长线交于点C,若CE=2,则图中阴影部分的面积是( )
如图,AB是⊙O的直径,点D、E是半圆的三等分点,AE、BD的延长线交于点C,若CE=2,则图中阴影部分的面积是( )| A. | $\frac{4}{3}$π-$\sqrt{3}$ | B. | π | C. | π-$\sqrt{3}$ | D. | $\sqrt{3}$ |
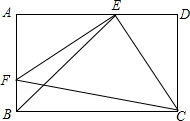 如图,E、F分别是矩形ABCD的边AD、AB上的点,若EF=EC,EF⊥EC,DC=$\sqrt{2}$,则BE的长为2.
如图,E、F分别是矩形ABCD的边AD、AB上的点,若EF=EC,EF⊥EC,DC=$\sqrt{2}$,则BE的长为2.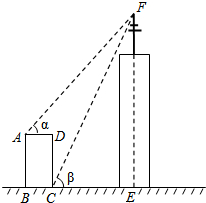 如图,某高楼顶部有一信号发射塔,小凡在矩形建筑物ABCD的A、C两点处测得塔顶F的仰角分别为α和β,AD=18m,CD=78m.
如图,某高楼顶部有一信号发射塔,小凡在矩形建筑物ABCD的A、C两点处测得塔顶F的仰角分别为α和β,AD=18m,CD=78m.