题目内容
8.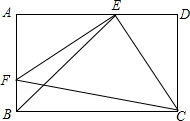 如图,E、F分别是矩形ABCD的边AD、AB上的点,若EF=EC,EF⊥EC,DC=$\sqrt{2}$,则BE的长为2.
如图,E、F分别是矩形ABCD的边AD、AB上的点,若EF=EC,EF⊥EC,DC=$\sqrt{2}$,则BE的长为2.
分析 根据矩形的性质和已知条件可证明△AEF≌△DCE,可证得AE=DC=AB,在Rt△ABE中由勾股定理可求得BE的长.
解答 解:在矩形ABCD中,∠A=∠D=90°,AB=CD=$\sqrt{2}$,
∴∠AFE+∠AEF=90°,
∵EF⊥EC,
∴∠FEC=90°,
∴∠AEF+∠DEC=90°,
∴∠AFE=∠DEC,
在△AEF和△DCE中,$\left\{\begin{array}{l}{∠A=∠D}&{\;}\\{∠AFE=∠DEC}&{\;}\\{EF=EC}&{\;}\end{array}\right.$,
∴△AEF≌△DCE(AAS),
∴AE=DC=$\sqrt{2}$=AB,
在Rt△ABE中,BE=$\sqrt{A{E}^{2}+A{B}^{2}}$=$\sqrt{2}$AB=2;
故答案为:2.
点评 本题主要考查矩形的性质、全等三角形的判定和性质、勾股定理;熟练掌握矩形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
19.下列运算正确的是( )
| A. | $\sqrt{8}$-$\sqrt{2}$=$\sqrt{2}$ | B. | $\sqrt{4\frac{1}{9}}$=2$\frac{1}{3}$ | C. | $\sqrt{5}$-$\sqrt{3}$=$\sqrt{2}$ | D. | $\sqrt{(2-\sqrt{5})^{2}}$=2-$\sqrt{5}$ |
16.已知等腰三角形两边长分别为3和5,第三边是方程x2-5x+6=0的解,则这个三角形的周长是( )
| A. | 9 | B. | 10 | C. | 11 | D. | 14 |
13.下列计算正确的是( )
| A. | 3a2-a2=2 | B. | a6•a3=a18 | C. | (a3)3=a6 | D. | x3÷x-1=x4 |
 如图,在正方形ABCD中,AB=$\sqrt{2}$,点P为边AB上一动点(不与A、B重合),过A、P在正方形内部作正方形APEF,交边AD于F点,连接DE、EC,当△CDE为等腰三角形时,AP=$\sqrt{2}$-1或$\frac{\sqrt{2}}{2}$.
如图,在正方形ABCD中,AB=$\sqrt{2}$,点P为边AB上一动点(不与A、B重合),过A、P在正方形内部作正方形APEF,交边AD于F点,连接DE、EC,当△CDE为等腰三角形时,AP=$\sqrt{2}$-1或$\frac{\sqrt{2}}{2}$.