题目内容
 如图,在四边形ABCD中,E、F分别是AD、BC的中点,G、H分别是BD、AC的中点,当AB、CD满足什么条件时,有EF⊥GH?请说明你的理由.
如图,在四边形ABCD中,E、F分别是AD、BC的中点,G、H分别是BD、AC的中点,当AB、CD满足什么条件时,有EF⊥GH?请说明你的理由.考点:中点四边形
专题:
分析:当AB=CD时,有EF⊥GH,连接GE、GF、HF、EH,根据三角形的中位线定理即可证得EG=GF=FH=EH,则四边形EFGH是菱形,利用菱形的性质即可证得.
解答:解:当AB=CD时,有EF⊥GH,
连接GE、GF、HF、EH.
∵E、G分别是AD、BD的中点,
∴EG=
AB,
同理HF=
CD,FG=
CD,EH=
CD,
又∵AB=CD
∴EG=GF=FH=EH
∴四边形EFGH是菱形.
∴EF⊥GH.
连接GE、GF、HF、EH.

∵E、G分别是AD、BD的中点,
∴EG=
| 1 |
| 2 |
同理HF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
又∵AB=CD
∴EG=GF=FH=EH
∴四边形EFGH是菱形.
∴EF⊥GH.
点评:本题考查了三角形的中位线定理,菱形的判定与性质,正确证明四边形EFGH是菱形是关键.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
 如图,△ABC中AC=4,BC=3,AB=5,求△ABC的面积.
如图,△ABC中AC=4,BC=3,AB=5,求△ABC的面积.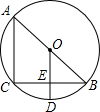 如图,AB是⊙O的直径,BC是弦,OD⊥BC,垂足为E,交⊙O于D,连接AC.
如图,AB是⊙O的直径,BC是弦,OD⊥BC,垂足为E,交⊙O于D,连接AC. 如图在平行四边形ABCD中,AC交BD于点O,AE⊥BD,CF⊥BD,垂足分别为E、F,求证:四边形AECF为平行四边形.
如图在平行四边形ABCD中,AC交BD于点O,AE⊥BD,CF⊥BD,垂足分别为E、F,求证:四边形AECF为平行四边形.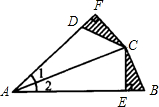 如图,在△ABC中,CE⊥AB于E,在△ABC外作∠CAD=∠CAB,过C作CF⊥AD,交AD的延长线于F,且∠FDC=∠B,求证:BE=DF.
如图,在△ABC中,CE⊥AB于E,在△ABC外作∠CAD=∠CAB,过C作CF⊥AD,交AD的延长线于F,且∠FDC=∠B,求证:BE=DF.