题目内容
17. 如图,在△ABC中,D是BC边的中点,E、F分别在AD及其延长线上,CE∥BF,连接BE、CF.
如图,在△ABC中,D是BC边的中点,E、F分别在AD及其延长线上,CE∥BF,连接BE、CF.(1)求证:△BDF≌△CDE;
(2)当△ABC满足什么条件时,四边形BFCE是菱形?
分析 (1)由平行线的性质得出∠DBF=∠DCE,由ASA即可证明△BDF≌△CDE;
(2)由△CDE≌△BDF,得出DE=DF,证出四边形BFCE是平行四边形,再由AB=AC,根据等腰三角形的三线合一性质得出EF⊥BC,即可证出四边形BFCE是菱形.
解答 (1)证明:∵D是BC的中点,
∴BD=CD,
∵CE∥BF,
∴∠DBF=∠DCE,
在△BDF和△CDE中,$\left\{\begin{array}{l}{∠DBF=∠DCE}&{\;}\\{BD=CD}&{\;}\\{∠BDF=∠CDE}&{\;}\end{array}\right.$,
∴△BDF≌△CDE(ASA);
(2)解:当△ABC是等腰三角形,即AB=AC时,四边形BFCE是菱形;理由如下:
∵△BDF≌△CDE,
∴DF=DE,
∵BD=CD,
∴四边形BFCE是平行四边形,
在△ABC中,∵AB=AC,BD=CD,
∴AD⊥BC,
即EF⊥BC
∴四边形BFCE是菱形.
点评 本题考查了全等三角形的判定与性质、等腰三角形的性质、菱形的判定;熟练掌握全等三角形的判定与性质,并能进行推理论证是解决问题的关键.

练习册系列答案
相关题目
9.通常情况下,若y是关于x的函数,则y与x的函数关系式可记作y=f(x).如y=$\frac{1}{2}$x+3记作f(x)=$\frac{1}{2}$x+3,当x=2时,f(2)=$\frac{1}{2}$×2+3=4.下列四个函数中,满足f(a+b)=f(a)+f(b)的函数是( )
| A. | y=$\frac{\sqrt{3}}{x}$ | B. | y=-2x-6 | C. | y=3x | D. | y=$\frac{1}{2}{x}^{2}+3x+4$ |
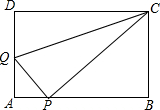 如图,在矩形ABCD中,AB=5,AD=3,点P是AB边上一点(不与A,B重合),连接CP,过点P作PQ⊥CP交AD边于点Q,连接CQ.
如图,在矩形ABCD中,AB=5,AD=3,点P是AB边上一点(不与A,B重合),连接CP,过点P作PQ⊥CP交AD边于点Q,连接CQ.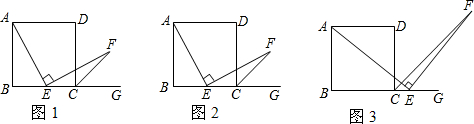

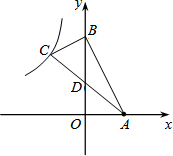 如图,A(3,0),B(0,6),BC⊥AB且D为AC中点,双曲线y=$\frac{k}{x}$过点C,则k=-$\frac{27}{2}$.
如图,A(3,0),B(0,6),BC⊥AB且D为AC中点,双曲线y=$\frac{k}{x}$过点C,则k=-$\frac{27}{2}$.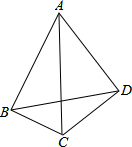 在数学活动中,我们已经学习了四点共圆的条件:如果一个四边形对角互补,那么这个四边形的四个顶点在同一个圆上,简称“四点共圆”.如图,已知四边形ABCD,AD=4,CD=3,AC=5,cos∠BCA=sin∠BAC=$\frac{1}{2}$,求∠BDC的大小.
在数学活动中,我们已经学习了四点共圆的条件:如果一个四边形对角互补,那么这个四边形的四个顶点在同一个圆上,简称“四点共圆”.如图,已知四边形ABCD,AD=4,CD=3,AC=5,cos∠BCA=sin∠BAC=$\frac{1}{2}$,求∠BDC的大小.