题目内容
1．（1）|2-tan60°|-（π-3.14）0+（-$\frac{1}{2}$）-2+$\frac{1}{2}$$\sqrt{12}$．（2）已知：y=y1+y2，y1与x2成正比例，y2与x成反比例，且x=1时，y=3；x=-2时，y=1．求x=-3时，y的值．
分析 （1）原式第一项利用特殊角的三角函数值及绝对值的代数意义化简，第二项利用零指数幂法则计算，第三项利用负整数指数幂法则计算，最后一项化为最简二次根式，计算即可得到结果；
（2）根据y1与x2成正比例，y2与x成反比例，分别设出y1与y2，进而表示出y与x解析式，把x与y的两对值代入计算确定出解析式，即可求出x=-3时y的值．
解答 解：（1）原式=2-$\sqrt{3}$-1+4+$\sqrt{3}$=5；
（2）∵y1与x2成正比例，y2与x成反比例
∴设y1=k1x2，y2=$\frac{{k}_{2}}{x}$，即y=k1x2+$\frac{{k}_{2}}{x}$，
把x=1，y=3，x=-1，y=（1分）别代入上式得$\left\{\begin{array}{l}{3={k}_{1}+{k}_{2}}\\{1={k}_{1}-{k}_{2}}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{{k}_{1}=2}\\{{k}_{2}=1}\end{array}\right.$，即y=2x2+$\frac{1}{x}$，
当x=-3时，y=2×（-3）2-$\frac{1}{3}$=17$\frac{2}{3}$．
点评 此题考查了实数的运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
选作题（请从以下两个小题中任选一题作答，若多选，则按所选的第一题计分．）
9．通常情况下，若y是关于x的函数，则y与x的函数关系式可记作y=f（x）．如y=$\frac{1}{2}$x+3记作f（x）=$\frac{1}{2}$x+3，当x=2时，f（2）=$\frac{1}{2}$×2+3=4．下列四个函数中，满足f（a+b）=f（a）+f（b）的函数是（ ）
| A． | y=$\frac{\sqrt{3}}{x}$ | B． | y=-2x-6 | C． | y=3x | D． | y=$\frac{1}{2}{x}^{2}+3x+4$ |
16．某通讯公司推出了A、B两种不同上网计费方式如下表：
项目
设一个月内移动电话的流量为tMB（t≥0），根据要求回答下列问题．
（1）用含t的式子填写下表：
（2）当t为何值时，两种计费方式的费用相等；
（3）当50＜t＜100时，你认为选择哪种计费方式更省钱，并说明理由．
项目
| 项目/计费方式 | 月租费（元） | 限流量（MB） | 超流量（元/MB） |
| A | 5 | 30 | 0.5 |
| B | 10 | 70 | 1 |
（1）用含t的式子填写下表：
| 流量/计费方式 | t≥30 | 30≤t≤70 | t＞70 |
| A种计费（元） | 5 | 0.5t-10 | 0.5t-10 |
| B种计费（元） | 10 | 10 | t-60 |
（3）当50＜t＜100时，你认为选择哪种计费方式更省钱，并说明理由．
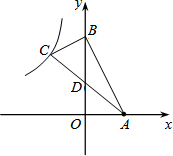如图，A（3，0），B（0，6），BC⊥AB且D为AC中点，双曲线y=$\frac{k}{x}$过点C，则k=-$\frac{27}{2}$．
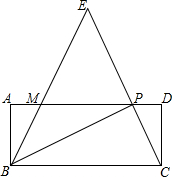如图，矩形ABCD中，P是边AD上的一动点，连接BP、CP，过点B作射线交线段CP的延长线于点E，交AD边于点M，且使得∠ABE=∠CBP，