题目内容
20.解方程(组):(1)$\frac{1}{3x}$=$\frac{1}{2x}$+2;
(2)$\left\{\begin{array}{l}{3x-4(x-y)=2}\\{x-y=1}\end{array}\right.$.
分析 (1)根据等式的性质,可得整式方程,根据解整式方程,可得答案;
(2)根据代入消元法,可得答案.
解答 解:(1)去分母,得
2=3+12x,
解得x=-$\frac{1}{12}$,
经检验:x=-$\frac{1}{12}$是原分式方程的解;
(2)
$\left\{\begin{array}{l}{3x-4(x-y)=2①}\\{x-y=1②}\end{array}\right.$,
把②代入①,得
x=2,
把x=2代入②得y=1,
原方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$.
点评 本题考查了解分式方程,利用等式的性质得出整式方程是解题关键.

练习册系列答案
相关题目
10.下列计算正确的是( )
| A. | (-a)6÷a3=a3 | B. | a2•a3=a6 | C. | (2a4)4=16a8 | D. | a+a2=2a3 |


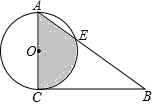 如图,在△ABC中,∠ACB=90°,AC=2,∠B=30°,以AC为直径作圆交AB于点E,则图中阴影部分的面积为$\frac{1}{3}$π+$\frac{\sqrt{3}}{4}$.
如图,在△ABC中,∠ACB=90°,AC=2,∠B=30°,以AC为直径作圆交AB于点E,则图中阴影部分的面积为$\frac{1}{3}$π+$\frac{\sqrt{3}}{4}$.