题目内容
6. 如图,抛物线y=ax2+bx+2与x轴交于点A(-1,0),B(4,0)两点,与y轴交于点C,与过点C且平行x轴的直线交于另一点D.
如图,抛物线y=ax2+bx+2与x轴交于点A(-1,0),B(4,0)两点,与y轴交于点C,与过点C且平行x轴的直线交于另一点D.(1)求a、b的值及D的坐标;
(2)若直线l过点M(0,-$\frac{3}{7}$),且平分四边形ABDC的面积,求直线l的解析式.
分析 (1)把A,B坐标代入抛物线解析式即可求出a,b的值,再令x=0求出C点坐标,进一步求出D点坐标即可;
(2)设出l的解析式,表示出与AB,CD的交点,根据平分面积列方程求解即可.
解答 解:(1)∵y=ax2+bx+2与x轴交于点A(-1,0),B(4,0)两点,
∴$\left\{\begin{array}{l}{a-b+2=0}\\{16a+4b+2=0}\end{array}\right.$,
解得:a=$-\frac{1}{2}$,b=$\frac{3}{2}$;
∴y=${-\frac{1}{2}x}^{2}+\frac{3}{2}x+2$,
当x=0时,y=2,
∴点C(0,2),
当y=2时,${-\frac{1}{2}x}^{2}+\frac{3}{2}x+2$=2,
解得:x=0,或x=3,
∴点D(3,2);
(2)如图1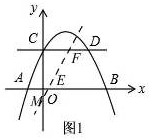
直线l过点M(0,-$\frac{3}{7}$),
可设l:y=kx$-\frac{3}{7}$,交AB于点E,交CD于点F,
当y=0时,x=$\frac{\frac{3}{7}}{k}$,当y=2时,x=$\frac{\frac{17}{7}}{k}$,
∴FD=3-$\frac{\frac{17}{7}}{k}$,BE=4-$\frac{\frac{3}{7}}{k}$,
由题意可得:FD+BM=$\frac{1}{2}(AB+CD)$=$\frac{1}{2}×(5+3)$=4,
∴3-$\frac{\frac{17}{7}}{k}$+4-$\frac{\frac{3}{7}}{k}$=4,
解得:k=$\frac{20}{21}$;
∴直线l的解析式为:y=$\frac{20}{21}$x-$\frac{3}{7}$.
点评 此题主要考查抛物线的图象交点问题,会用点求解析式,会待定直线解析式解决均分图形面积是解题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | x-2y=4 | B. | xy=4 | C. | 3y-1=4 | D. | $\frac{1}{4}x-4$ |
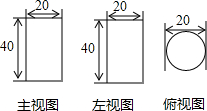 如图,是一个几何体的三视图,它的几何体表面积为900π.
如图,是一个几何体的三视图,它的几何体表面积为900π.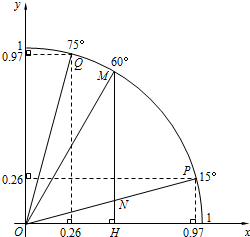 如图,点P、M、Q在半径为1的⊙O上,根据已学知识和图中数据(0.97、0.26为近似数),解答下列问题:
如图,点P、M、Q在半径为1的⊙O上,根据已学知识和图中数据(0.97、0.26为近似数),解答下列问题: