题目内容
 如图,过原点O任意引一直线交y=
如图,过原点O任意引一直线交y=| 1 |
| x |
| 4 |
| x |
| 4 |
| x |
考点:反比例函数系数k的几何意义
专题:
分析:设A(a,
),根据题意则可求出C(4a,
),B(2a,
),继而根据三角形的面积公式即可求得△ABC的面积.
| 1 |
| a |
| 1 |
| a |
| 2 |
| a |
解答:
解:设A(a,
),
∵AC∥x轴,
∴C(4a,
),
设直线OA的解析式为y=kx,
∴k=a2,
∴直线OA的解析式为y=a2x,
解
,解得
,
,
∴B(2a,
),
∴S△ABC=
(4a-a)(
-
)=
.
故答案为
.
| 1 |
| a |
∵AC∥x轴,
∴C(4a,
| 1 |
| a |
设直线OA的解析式为y=kx,
∴k=a2,
∴直线OA的解析式为y=a2x,
解
|
|
|
∴B(2a,
| 2 |
| a |
∴S△ABC=
| 1 |
| 2 |
| 2 |
| a |
| 1 |
| a |
| 3 |
| 2 |
故答案为
| 3 |
| 2 |
点评:此题考查了反比例函数的k的几何意义,解答本题的关键是分别表示出A、B、C点的坐标,利用面积公式求解△ABC的面积.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
 如图,已知AB∥CD,EF∥MN,∠1=115°,
如图,已知AB∥CD,EF∥MN,∠1=115°,
 如图,在四边形ABCD中,∠1=∠2,∠3=∠4,∠B=∠D,AF=CE,AB∥CD.
如图,在四边形ABCD中,∠1=∠2,∠3=∠4,∠B=∠D,AF=CE,AB∥CD. 某班在一次测试中,一道计算题(满分5分)的得分情况如图.则这题得分的平均数是
某班在一次测试中,一道计算题(满分5分)的得分情况如图.则这题得分的平均数是
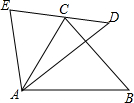 如图,E、C、D三点在一条直线上,AE=AC,AD=AB,∠EAC=∠DAB.求证:△EAD≌△CAB.
如图,E、C、D三点在一条直线上,AE=AC,AD=AB,∠EAC=∠DAB.求证:△EAD≌△CAB.