题目内容
△ABC中，AB=10，BC=16，D为AC的中点，则中线BD的取值范围为 ．
考点：全等三角形的判定与性质,三角形三边关系
专题：
分析：延长BD到点E，使BD=DE，连接AE，可证明△ADE≌△CDB，可得AE=BC=16，在△ABE中利用三角形三边关系可求得BE的范围，可求得BD的取值范围．
解答：
解：
如图，延长BD到点E，使BD=DE，连接AE，
在△ADE和△CDB中
∴△ADE≌△CDB（SAS），
∴AE=BC=16，且AB=10，
在△ABE中，由三角形三边关系可得AE-AB＜BE＜AE+AB，
即16-10＜BE＜16+10，
∴6＜BE＜26，
∴6＜2BD＜26，
∴3＜BD＜13，
故答案为：3＜BD＜13．
解：如图，延长BD到点E，使BD=DE，连接AE，
在△ADE和△CDB中
|
∴△ADE≌△CDB（SAS），
∴AE=BC=16，且AB=10，
在△ABE中，由三角形三边关系可得AE-AB＜BE＜AE+AB，
即16-10＜BE＜16+10，
∴6＜BE＜26，
∴6＜2BD＜26，
∴3＜BD＜13，
故答案为：3＜BD＜13．
点评：本题主要考查全等三角形的判定和性质及三角形的三边关系，掌握全等三角形的判定方法（即SSS、SAS、ASA、AAS和HL）和全等三角形的性质（对应边、对应角相等）是解题的关键．
练习册系列答案
相关题目
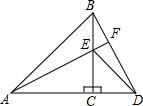如图，△ACB和△ECD都是等腰直角三角形，A、C、D三点在同一直线上，连接BD、AE，并延长AE交BD于F．
如图所示，△ABC中，AB=BC=AC，BD=CE，AD与BE相交于点P，则∠APE的度数是（ ）| A、45° | B、55° |
| C、75° | D、60° |
如图，在四边形ABCD中，∠1=∠2，∠3=∠4，∠B=∠D，AF=CE，AB∥CD．
某班在一次测试中，一道计算题（满分5分）的得分情况如图．则这题得分的平均数是
