题目内容
12.在矩形ABCD中,AB=8,BC=7,以CD为边在矩形外部作△CDE,且S△CDE=16,连接BE,则BE+DE的最小值为( )| A. | 15 | B. | 16 | C. | 17 | D. | 18 |
分析 由S△CDE=$\frac{1}{2}$DC•h=16,得出三角形的高h=4,在直线DC外作直线l∥CD,且两直线间的距离为4,延长AD至P是DP=8,则P、D关于直线l对称,连接PB,交直线l于E,连接DE、CE,则S△CDE=16,此时BE+DE=PB,根据两点之间线段最短可知BE+DE的最小值为PB;然后根据勾股定理即可求得.
解答 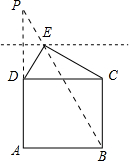 解;∵在矩形ABCD中,AB=8,BC=7,
解;∵在矩形ABCD中,AB=8,BC=7,
∴DC=8,AD=7,
∵S△CDE=$\frac{1}{2}$DC•h=16,
∴h=4,
在直线DC外作直线l∥CD,且两直线间的距离为4,延长AD至P是DP=8,则P、D关于直线l对称,连接PB,交直线l于E,连接DE、CE,则S△CDE=16,此时BE+DE=PB,根据两点之间线段最短可知BE+DE的最小值为PB;
∵AD=7,PD=8,
∴PA=15,
∵AB=8,
∴PB=$\sqrt{P{A}^{2}+A{B}^{2}}$=17,
∴BE+DE的最小值为17;
故选C.
点评 本题考查了轴对称-最短路线问题以及勾股定理的应用,根据题意作出点E是解题的关键.

练习册系列答案
相关题目
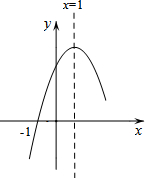 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,且对称轴为直线x=1,点B坐标为(-1,0).则下面的四个结论:①2a+b=0;②8a+c<0;③abc>0;④当y<0时,x<-1或x>2,⑤对任意实数m,m(am+b)≤a+b.其中正确的结论有( )个.
如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,且对称轴为直线x=1,点B坐标为(-1,0).则下面的四个结论:①2a+b=0;②8a+c<0;③abc>0;④当y<0时,x<-1或x>2,⑤对任意实数m,m(am+b)≤a+b.其中正确的结论有( )个.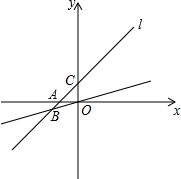 直线l经过(2,3)和(-2,-1)两点,它还与x轴交于A点,与y轴交于C点,与经过原点的直线OB交于第三象限的B点,且∠ABO=30°.求:
直线l经过(2,3)和(-2,-1)两点,它还与x轴交于A点,与y轴交于C点,与经过原点的直线OB交于第三象限的B点,且∠ABO=30°.求:
 的结果是( )
的结果是( )