题目内容
16．正方形的边长与对角线的比是$\sqrt{2}$：2；等边三角形的边长与高的比是2：$\sqrt{3}$．分析 正方形的边长与对角线的比=sin45°=$\frac{\sqrt{2}}{2}$，即可得出结果；等边三角形的高与边长的比=sin60°=$\frac{\sqrt{3}}{2}$，即可得出结果．
解答 解：如图1所示：
∵四边形ABCD是正方形，
∴AB=BC=CD=DA，AC=BD，∠BAD=90°，
∴∠ABD=45°，
∴AB：BD=sin45°=$\sqrt{2}$：2；
故答案为：$\sqrt{2}$：2；
如图2所示：∵△EFG是等边三角形，EH是高，
∴EF=FG=GE，∠EFH=60°，∠EHF=90°，
∴sin60°=$\frac{EH}{EF}$=$\frac{\sqrt{3}}{2}$，
∴EF：EH=2：$\sqrt{3}$；
故答案为：2：$\sqrt{3}$．
点评 本题考查了正方形的性质、等边三角形的性质、三角函数的运用；熟练掌握正方形和等边三角形的性质，运用三角函数进行计算是解决问题的关键．
练习册系列答案
手拉手全优练考卷系列答案
相关题目
11．
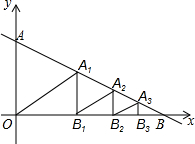如图，已知直线y=-$\frac{1}{2}$x+2与x轴交于点B，与y轴交于点A．过线段AB的中点A1做A1B1⊥x轴于点B1，过线段A1B的中点A2作A2B2⊥x轴于点B2，过线段A2B的中点A3作A3B3⊥x轴于点B3…，以此类推，则△AnBnBn-1的面积为（ ）
如图，已知直线y=-$\frac{1}{2}$x+2与x轴交于点B，与y轴交于点A．过线段AB的中点A1做A1B1⊥x轴于点B1，过线段A1B的中点A2作A2B2⊥x轴于点B2，过线段A2B的中点A3作A3B3⊥x轴于点B3…，以此类推，则△AnBnBn-1的面积为（ ）| A． | $\frac{1}{{2}^{n-1}}$ | B． | $\frac{1}{{2}^{n}}$ | C． | $\frac{1}{{4}^{n-1}}$ | D． | $\frac{1}{{4}^{n}}$ |
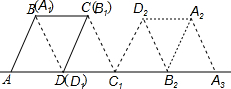如图，在菱形ABCD中，AB=4cm，∠BAD=60°，将菱形ABCD绕点D按顺时针方向作第一次旋转得到菱形A1B1C1D1，使点C落在点C1的位置，再将其绕点C1按顺时针方向作第二次旋转，使点B1落在点B2的位置…如此旋转下去，当点A2落在A3的位置时，点A在旋转过程中经过的路径长为$\frac{8+8\sqrt{3}}{3}$cm．
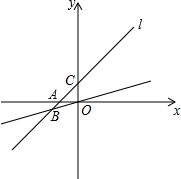直线l经过（2，3）和（-2，-1）两点，它还与x轴交于A点，与y轴交于C点，与经过原点的直线OB交于第三象限的B点，且∠ABO=30°．求：
