题目内容
1. 如图,点P在半径为3的⊙O内,OP=$\sqrt{3}$,点A为⊙O上一动点,弦AB过点P,则AB最长为6,AB最短为2$\sqrt{6}$.
如图,点P在半径为3的⊙O内,OP=$\sqrt{3}$,点A为⊙O上一动点,弦AB过点P,则AB最长为6,AB最短为2$\sqrt{6}$.
分析 过P点的最长的弦为直径,最短的弦为垂直于过P点的直径的弦,则根据垂径定理得到AP=BP$\frac{1}{2}$AB,然后根据勾股定理可计算出AP的长.
解答 解:AB为过P点的直径时,则AB最长为6,
当OP⊥AB时,AB为过P点的最短弦,
∵OP⊥AB,
在Rt△APO中,
AP=PB=$\frac{1}{2}$AB=$\sqrt{{OA}^{2}{-OP}^{2}}$=$\sqrt{{3}^{2}{-(\sqrt{3})}^{2}}$=$\sqrt{6}$,
∴AB=2$\sqrt{6}$,
故答案为:2$\sqrt{6}$,6.
点评 本题主要考查了垂径定理,勾股定理,能够理解过P点的最长的弦为直径,最短的弦为垂直于过P点的直径的弦是解答此题的关键.

练习册系列答案
相关题目
14.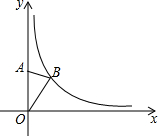 如图,在平面直角坐标系中,点A是y轴正半轴上的一个定点,点B是反比例函数y=$\frac{k}{x}$(k为常数)在第一象限内图象上的一个动点.当点B的纵坐标逐渐增大时,△OAB的面积( )
如图,在平面直角坐标系中,点A是y轴正半轴上的一个定点,点B是反比例函数y=$\frac{k}{x}$(k为常数)在第一象限内图象上的一个动点.当点B的纵坐标逐渐增大时,△OAB的面积( )
 如图,在平面直角坐标系中,点A是y轴正半轴上的一个定点,点B是反比例函数y=$\frac{k}{x}$(k为常数)在第一象限内图象上的一个动点.当点B的纵坐标逐渐增大时,△OAB的面积( )
如图,在平面直角坐标系中,点A是y轴正半轴上的一个定点,点B是反比例函数y=$\frac{k}{x}$(k为常数)在第一象限内图象上的一个动点.当点B的纵坐标逐渐增大时,△OAB的面积( )| A. | 逐渐减小 | B. | 逐渐增大 | C. | 先增大后减小 | D. | 不变 |
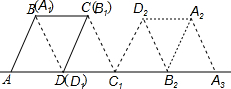 如图,在菱形ABCD中,AB=4cm,∠BAD=60°,将菱形ABCD绕点D按顺时针方向作第一次旋转得到菱形A1B1C1D1,使点C落在点C1的位置,再将其绕点C1按顺时针方向作第二次旋转,使点B1落在点B2的位置…如此旋转下去,当点A2落在A3的位置时,点A在旋转过程中经过的路径长为$\frac{8+8\sqrt{3}}{3}$cm.
如图,在菱形ABCD中,AB=4cm,∠BAD=60°,将菱形ABCD绕点D按顺时针方向作第一次旋转得到菱形A1B1C1D1,使点C落在点C1的位置,再将其绕点C1按顺时针方向作第二次旋转,使点B1落在点B2的位置…如此旋转下去,当点A2落在A3的位置时,点A在旋转过程中经过的路径长为$\frac{8+8\sqrt{3}}{3}$cm.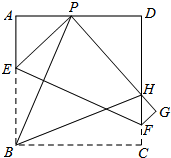 如图,现有一张边长为4的正方形纸片ABCD,点P为正方形AD边上的一点(不与点A、点D重合),将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH.
如图,现有一张边长为4的正方形纸片ABCD,点P为正方形AD边上的一点(不与点A、点D重合),将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH.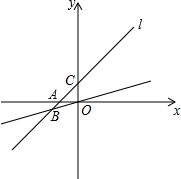 直线l经过(2,3)和(-2,-1)两点,它还与x轴交于A点,与y轴交于C点,与经过原点的直线OB交于第三象限的B点,且∠ABO=30°.求:
直线l经过(2,3)和(-2,-1)两点,它还与x轴交于A点,与y轴交于C点,与经过原点的直线OB交于第三象限的B点,且∠ABO=30°.求: 的顶点坐标是___________
的顶点坐标是___________