题目内容
19.已知弓形弦长等于$\sqrt{2}$R(R为半径),则此弓形的面积为($\frac{π-2}{4}$)R2或($\frac{3π+2}{4}$)R2.分析 根据题意分别画出图形,进而利用三角形和扇形面积求法进而得出答案.
解答  解:如图1所示:
解:如图1所示:
∵AO=BO=R,AB=$\sqrt{2}$R,
∴∠AOB=90°,
∴S△AOB=$\frac{1}{2}$R2,
S扇形AOB=$\frac{90π{R}^{2}}{360}$=$\frac{π{R}^{2}}{4}$,
∴此弓形的面积为:$\frac{π{R}^{2}}{4}$-$\frac{{R}^{2}}{2}$=($\frac{π-2}{4}$)R2,
如图2所示:
∵AO=BO=R,AB=$\sqrt{2}$R,
∴∠AOB=90°,
∴S△AOB=$\frac{1}{2}$R2,
S扇形AOB=$\frac{270π{R}^{2}}{360}$=$\frac{3π{R}^{2}}{4}$,
∴此弓形的面积为:$\frac{3π{R}^{2}}{4}$+$\frac{{R}^{2}}{2}$=($\frac{3π+2}{4}$)R2,
综上所述:此弓形的面积为:($\frac{π-2}{4}$)R2或($\frac{3π+2}{4}$)R2.
故答案为:($\frac{π-2}{4}$)R2或($\frac{3π+2}{4}$)R2.
点评 本题考查了扇形面积求法以及三角形面积求法等知识,利用分类讨论得出是解题关键.

练习册系列答案
相关题目
 如图,在?ABCD中,AC=4cm,BD=6cm,对角线AC、BD相交于点O,AC⊥AB,求?ABCD的周长.
如图,在?ABCD中,AC=4cm,BD=6cm,对角线AC、BD相交于点O,AC⊥AB,求?ABCD的周长.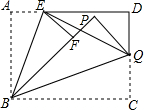 如图,在矩形ABCD中,AB=4,BC=6,点E是AD上一点,把∠A沿BE折叠,使点A落在F处,点Q是CD上一点,将∠C沿BQ折叠,点C恰好落在直线BF上,若∠BQE=45°,则AE=2.
如图,在矩形ABCD中,AB=4,BC=6,点E是AD上一点,把∠A沿BE折叠,使点A落在F处,点Q是CD上一点,将∠C沿BQ折叠,点C恰好落在直线BF上,若∠BQE=45°,则AE=2.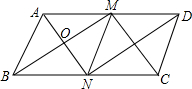 如图,在?ABCD中,M,N分别是AD,BC的中点,连接AN,BM,CM,DN,AN与BM交于点O.
如图,在?ABCD中,M,N分别是AD,BC的中点,连接AN,BM,CM,DN,AN与BM交于点O.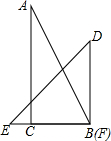 一副直角三角板按如图所示摆放一起,使等腰三角板DEF的直角顶点F与另一块直角三角板ABC的锐角顶点B(∠B=60°)重合,直角边BC与EF重合,此时两块直角三角板的斜边AB与DE的夹角(夹角指锐角或直角)是75°.
一副直角三角板按如图所示摆放一起,使等腰三角板DEF的直角顶点F与另一块直角三角板ABC的锐角顶点B(∠B=60°)重合,直角边BC与EF重合,此时两块直角三角板的斜边AB与DE的夹角(夹角指锐角或直角)是75°. 如图,在△ABC中,∠A=60°,BC=10,BO平分∠ABC,CO平分∠ACB,MN经过点O与AB,AC相交于点M,N,且MN∥BC,△AMN的周长为18.
如图,在△ABC中,∠A=60°,BC=10,BO平分∠ABC,CO平分∠ACB,MN经过点O与AB,AC相交于点M,N,且MN∥BC,△AMN的周长为18.