题目内容
13.有五名射击运动员,教练为了分析他们成绩的波动程度,应选择下列统计量中的( )| A. | 方差 | B. | 中位数 | C. | 众数 | D. | 平均数 |
分析 根据各自的定义判断即可.
解答 解:有五名射击运动员,教练为了分析他们成绩的波动程度,应选择下列统计量中的方差,
故选A
点评 此题考查了统计量的选择,弄清方差表示的意义是解本题的关键.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
3.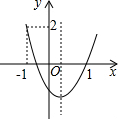 如图,二次函数y=ax2+bx+c的图象开口向上,图象经过点(-1,2)和点(1,0),且与y轴交于负半轴,给出下面四个结论:
如图,二次函数y=ax2+bx+c的图象开口向上,图象经过点(-1,2)和点(1,0),且与y轴交于负半轴,给出下面四个结论:
①abc<0;
②2a+b>0;
③a+c=1;
④a-b<2.
其中正确结论的有( )
 如图,二次函数y=ax2+bx+c的图象开口向上,图象经过点(-1,2)和点(1,0),且与y轴交于负半轴,给出下面四个结论:
如图,二次函数y=ax2+bx+c的图象开口向上,图象经过点(-1,2)和点(1,0),且与y轴交于负半轴,给出下面四个结论:①abc<0;
②2a+b>0;
③a+c=1;
④a-b<2.
其中正确结论的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
5. 已知直线a∥b,一块含30°角的直角三角尺如图放置.若∠1=25°,则∠2等于( )
已知直线a∥b,一块含30°角的直角三角尺如图放置.若∠1=25°,则∠2等于( )
 已知直线a∥b,一块含30°角的直角三角尺如图放置.若∠1=25°,则∠2等于( )
已知直线a∥b,一块含30°角的直角三角尺如图放置.若∠1=25°,则∠2等于( )| A. | 50° | B. | 55° | C. | 60° | D. | 65° |
2.在$\sqrt{3}$,$\frac{1}{2}$,0,-2这四个数中,为无理数的是( )
| A. | $\sqrt{3}$ | B. | $\frac{1}{2}$ | C. | 0 | D. | -2 |
8.用A、B两种原料配制成某种饮料,已知这两种原料的维生素C的含量及购买这两种原料的价格如表:
(1)若要配制这种饮料10千克,要求至少含有4000单位的维生素C,试求出所需A种原料最少多少千克?
(2)如要求购买A、B两种原料的费用不超过52元,试求出所需A种原料最多多少千克?
| 原料 维生素及价格 | A种原料 | B种原料 |
| 维生素C(单位/千克) | 600 | 100 |
| 原料价格(元/千克) | 6 | 4 |
(2)如要求购买A、B两种原料的费用不超过52元,试求出所需A种原料最多多少千克?
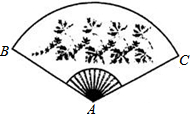 如图,扇形纸扇完全打开后,外侧两竹条AB,AC的夹角为120°,AB长为30厘米,则$\widehat{BC}$的长为20π厘米.(结果保留π)
如图,扇形纸扇完全打开后,外侧两竹条AB,AC的夹角为120°,AB长为30厘米,则$\widehat{BC}$的长为20π厘米.(结果保留π)