题目内容
1.解方程:(1)(3x-1)2=(x+1)2
(2)x2+2x-5=0.
分析 (1)先移项将方程右边化为0,用平方差公式将方程左边化为两个因式的乘积,令每个因式分别等于零,得到两个一元一次方程;解这两个一元一次方程,它们的解就是原方程的解;
(2)根据配方法的步骤先把常数项移到等号的右边,再在左右两边同时加上一次项系数2的一半的平方,配成完全平方的形式,然后开方即可.
解答 解:(1)(3x-1)2-(x+1)2=0,
(3x-1+x+1)(3x-1-x-1)=0,
4x(2x-2)=0,
即:4x=0或2x-2=0,
x1=0,x2=1;
(2)x2+2x=5,
x2+2x+1=6,
(x+1)2=6,
x+1=±$\sqrt{6}$,
x1=-1+$\sqrt{6}$,x2=-1-$\sqrt{6}$.
点评 本题考查了运用因式分解的方法以及配方法解一元二次方程,一元二次方程的解法有直接开平方方法,公式法,配方法,因式分解法等等,学生在平时的训练中,学会根据方程的特征,选择恰当的方法,提高解题效率.

练习册系列答案
相关题目
12.二元一次方程组$\left\{\begin{array}{l}{x+3y=2}\\{2x-3y=1}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=1}\\{y=\frac{1}{3}}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=1}\\{y=-\frac{1}{3}}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=3}\\{y=-\frac{1}{3}}\end{array}\right.$ |
8.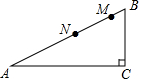 如图,∠C=90°,AC=12,CB=5,AM=AC,BN=BC,则MN的长是( )
如图,∠C=90°,AC=12,CB=5,AM=AC,BN=BC,则MN的长是( )
 如图,∠C=90°,AC=12,CB=5,AM=AC,BN=BC,则MN的长是( )
如图,∠C=90°,AC=12,CB=5,AM=AC,BN=BC,则MN的长是( )| A. | 2 | B. | 2.6 | C. | 3 | D. | 4 |

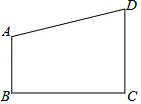 在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个三角形,剩下的部分是如图所示的四边形,AB∥CD,CD⊥BC于C,且AB、BC、CD边长分别为2,4,3,则原直角三角形纸片的斜边长是4$\sqrt{5}$或10.
在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个三角形,剩下的部分是如图所示的四边形,AB∥CD,CD⊥BC于C,且AB、BC、CD边长分别为2,4,3,则原直角三角形纸片的斜边长是4$\sqrt{5}$或10.