题目内容
6.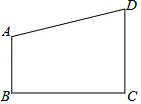 在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个三角形,剩下的部分是如图所示的四边形,AB∥CD,CD⊥BC于C,且AB、BC、CD边长分别为2,4,3,则原直角三角形纸片的斜边长是4$\sqrt{5}$或10.
在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个三角形,剩下的部分是如图所示的四边形,AB∥CD,CD⊥BC于C,且AB、BC、CD边长分别为2,4,3,则原直角三角形纸片的斜边长是4$\sqrt{5}$或10.
分析 先根据题意画出图形,再根据勾股定理求出斜边上的中线,最后即可求出斜边的长.
解答 解:①如图:因为AC=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
点A是斜边EF的中点,
所以EF=2AC=4$\sqrt{5}$,
②如图:
因为BD=$\sqrt{{3}^{2}+{4}^{2}}$=5,
点D是斜边EF的中点,
所以EF=2BD=10,
综上所述,原直角三角形纸片的斜边长是4$\sqrt{5}$或10,
故答案是:4$\sqrt{5}$或10.
点评 此题考查了图形的剪拼,解题的关键是能够根据题意画出图形,在解题时要注意分两种情况画图,不要漏解.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
17.菱形ABCD中,边长AB=2,∠A=45°,则菱形ABCD的面积是( )
| A. | 4 | B. | 2$\sqrt{2}$ | C. | 4$\sqrt{2}$ | D. | $\sqrt{2}$ |
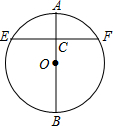 如图,在⊙O中,直径AB的长度为4a,3AC=CB,过点C作EF⊥AB,交⊙O于点E,F,则EF的长度为2$\sqrt{3}$a.
如图,在⊙O中,直径AB的长度为4a,3AC=CB,过点C作EF⊥AB,交⊙O于点E,F,则EF的长度为2$\sqrt{3}$a.