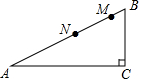如图.∠C=90°.AC=12.CB=5.AM=AC.BN=BC.则MN的长是( )A．2B．2.6C．3D．4 题目和参考答案——青夏教育精英家教网—

题目内容

8．

如图，∠C=90°，AC=12，CB=5，AM=AC，BN=BC，则MN的长是（　　）

A．

B．

2.6

C．

D．

分析由图示知：MN=AM+BN-AB，所以结合已知条件，根据勾股定理，求出AC的长即可解答．

解答解：在Rt△ABC中，根据勾股定理，可得
AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{1{2}^{2}+{5}^{2}}$=13，
又∵AC=12，BC=5，AM=AC，BN=BC，
∴AM=12，BN=5，
∴MN=AM+BN-AB=12+5-13=4．
故选：D．

点评本题主要考查了勾股定理的应用，找到关系MN=AM+BN-AB是解决问题的关键．

练习册系列答案

相关题目

1．解方程：
（1）（3x-1）²=（x+1）²
（2）x²+2x-5=0．

2．已知抛物线y=ax²+bx+c与抛物线y=3x²-6x+1关于y轴对称，求a、b、c的值．

19．为了节约用水，某市制定了以下用水收费标准：每户每月用水量不超过10立方米时，每立方米收费1.5元；每户每月用水量超过10立方米时，超过的部分按每立方米2.5元收取．设某户每月用水量为x立方米，应缴水费为y元．
（1）写出每户每月用水量未超过10立方米和超过10立方米时，y与x的函数关系式，y是x的一次函数吗？
（2）小明家十一月份的用水量为6立方米，则该月应缴多少水费？
（3）小刚家十一月份缴水费35元，则该月用水量是多少？

3．

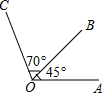已知：如图，∠AOB=45°，∠BOC=70°，求∠AOC的度数．
解：∵∠BOC=45，∠BOC=70°
∠AOC=∠AOB+∠BOC
=70°+45°
=115°．

13．用“*”表示一种运算，其意义是a*b=a-2b，如果x*（3*2）=3，则x=1．

20．

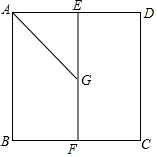在边长为1的正方形ABCD中，点E，F分别是边AD，BC的中点，动点G在线段EF上运动，将线段AG绕点G顺时针旋转60°得到线段HG．
（1）当点H与D不重合时，求∠HDA的度数；
（2）当动点G从E运动到F时，求点H运动的路线长．

17．

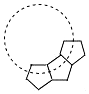如图，用若干个全等的正五边形可以拼成一个环状，如图是前3个正五边形的拼接情况，要完全拼成一个圆环还需要的正五边形个数是7．

18．若|x+y-5|与（x-y-1）²互为相反数，则x²-y²的值为（　　）

试题分类