题目内容
15．
如图，在△ABC中，AD为△ABC的中线，∠BAD=90°，∠CAD=30°，求证：AC=2AB．
分析 过D作DE∥AB交AC于E，由已知条件得到BD=CD，根据平行线等分线段定理得到AE=CE，根据三角形的中位线的性质得到AB=2DE，根据含30°角的直角三角形的性质得到AE=2DE，即可得到结论．
解答 解：
过D作DE∥AB交AC于E，
∵AD为△ABC的中线，
∴BD=CD，
∴AE=CE，
∴AB=2DE，
∵∠BAD=90°，
∴∠ADE=∠BAD=90°，
∵∠CAD=30°，
∴AE=2DE，
∴AB=AE，
∴AC=2AB．
点评 本题考查了含30°角的直角三角形的性质，三角形中位线的性质，平行线的性质，正确的作出辅助线是解题的关键．
练习册系列答案
相关题目
如图，∠A=∠D=90°，CD平分∠ACB，AB与CD相交于点E．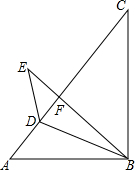
如图，在△ABC中，∠C为锐角，∠A=45°，AB=3$\sqrt{2}$，BC=5，D是AC边上一点，作点A关于直线BD的对称点E，连结DE、BE，BE与AC交于点F．若DE∥BC，则DF的长为$\frac{10}{7}$．