题目内容
20.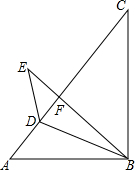 如图,在△ABC中,∠C为锐角,∠A=45°,AB=3$\sqrt{2}$,BC=5,D是AC边上一点,作点A关于直线BD的对称点E,连结DE、BE,BE与AC交于点F.若DE∥BC,则DF的长为$\frac{10}{7}$.
如图,在△ABC中,∠C为锐角,∠A=45°,AB=3$\sqrt{2}$,BC=5,D是AC边上一点,作点A关于直线BD的对称点E,连结DE、BE,BE与AC交于点F.若DE∥BC,则DF的长为$\frac{10}{7}$.
分析 过B作BM⊥AC于M,根据等腰直角三角形的性质得到AM=BM=3,CM=$\sqrt{B{C}^{2}-B{M}^{2}}$=4,AC=7,通过△BCM∽△ABC,得到$\frac{BC}{CF}=\frac{AC}{BC}$,求得CF=$\frac{25}{7}$,MF=CM-FM=$\frac{3}{7}$,AF=$\frac{24}{7}$,由于△DEF∽△BCF,根据相似三角形的性质得到$\frac{DE}{BC}=\frac{DF}{FC}$,设DF=x,则AD=DE=$\frac{24}{7}-x$,代入比例式即可得到结论.
解答 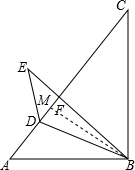 解:过B作BM⊥AC于M,
解:过B作BM⊥AC于M,
∵∠A=45°,$AB=3\sqrt{2}$,
∴AM=BM=3,CM=$\sqrt{B{C}^{2}-B{M}^{2}}$=4,AC=7,
∵∠BMC=∠ABC=90°,∠BCA=∠BCM,
∴△BCM∽△ABC,
∴$\frac{BC}{CF}=\frac{AC}{BC}$,
∴CF=$\frac{25}{7}$,
∴MF=CM-FM=$\frac{3}{7}$,
∴AF=$\frac{24}{7}$,
∵DE∥BC,
∴△DEF∽△BCF,
∴$\frac{DE}{BC}=\frac{DF}{FC}$,
设DF=x,则AD=DE=$\frac{24}{7}-x$,
∴$\frac{\frac{24}{7}-x}{5}=\frac{x}{\frac{25}{7}}$,
∴x=$\frac{10}{7}$,
∴DF=$\frac{10}{7}$.
故答案为:$\frac{10}{7}$.
点评 本题考查了相似三角形的判定和性质,直角三角形的性质,勾股定理,正确的作出辅助线是解题的关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
10. 如图,C、D是线段AB上的两点,且D是线段AC的中点,若AB=10cm,BC=4cm,则AD的长为( )
如图,C、D是线段AB上的两点,且D是线段AC的中点,若AB=10cm,BC=4cm,则AD的长为( )
 如图,C、D是线段AB上的两点,且D是线段AC的中点,若AB=10cm,BC=4cm,则AD的长为( )
如图,C、D是线段AB上的两点,且D是线段AC的中点,若AB=10cm,BC=4cm,则AD的长为( )| A. | 2cm | B. | 3cm | C. | 4cm | D. | 6cm |
9.计算($\sqrt{2}$)2的值正确的是( )
| A. | 2 | B. | $\sqrt{2}$ | C. | 4 | D. | 2$\sqrt{2}$ |
10.我海军某舰队在一次军事演习中,一核潜艇在海下时而上升,时而下降,核潜艇的初始位置在海平面下1500m,下面是核潜艇在某段时间内的运动情况(把上升记为“+”,下降记为“-”单位:m):
(1)现在核潜艇在什么位置?
(2)假如核潜艇上升或下降1m核动力装置所提供的能量相当于21L汽油燃烧所产生的能量,那么在这一时刻内,核动力装置所提供的能量相当于多少升汽油燃烧所产生的能量?
| 次数 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 第6次 |
| 运动升降 | -1200 | -20 | 30 | 20 | 60 | -80 |
(2)假如核潜艇上升或下降1m核动力装置所提供的能量相当于21L汽油燃烧所产生的能量,那么在这一时刻内,核动力装置所提供的能量相当于多少升汽油燃烧所产生的能量?
 如图,在△ABC中,AD为△ABC的中线,∠BAD=90°,∠CAD=30°,求证:AC=2AB.
如图,在△ABC中,AD为△ABC的中线,∠BAD=90°,∠CAD=30°,求证:AC=2AB.