题目内容
6．
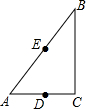如图，在△ABC中，∠C=90°，AC=6，BC=8，D、E分别是AC、AB的中点．若作半径为8的⊙B，则下列选项中的点在⊙B内的是（ ）| A． | 点A | B． | 点D | C． | 点C | D． | 点E |
分析 分别求出AB、BE、BC、BD的长，根据点与圆的位置关系的判断方法进行判断即可．
解答 解：∵∠C=90°，AC=6，BC=8，
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=10，
∴点A在⊙B外，
∵E是AB的中点，
∴BE=$\frac{1}{2}$AB=5，
∴点E在⊙B内，
∵BC=8，
∴点C在⊙B上，
∵BD＞BC，
∴点D在⊙B外，
故选：D．
点评 本题考查的是点与圆的位置关系的判断．关键要记住若半径为r，点到圆心的距离为d，则有：当d＞r时，点在圆外；当d=r时，点在圆上，当d＜r时，点在圆内．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
16．
如图正比例函数y=$\sqrt{3}$x与反比例函数y=$\frac{k}{x}$的图象在第一象限内交于点A，且AO=2，则k等于（ ）
如图正比例函数y=$\sqrt{3}$x与反比例函数y=$\frac{k}{x}$的图象在第一象限内交于点A，且AO=2，则k等于（ ）| A． | 1 | B． | $\sqrt{3}$ | C． | $\sqrt{2}$ | D． | 2 |
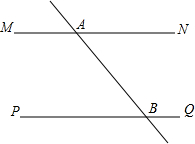如图，公路MN∥PQ，公路AB交公路MN于A，交公路PQ于B，若要建一汽车旅店到三条公路的距离相等，则可供选择的地址有（ ）
梯形ABCD中，DC∥AB，BC=10，且MN∥PQ∥AB，DM=MP=2PA，则CN=4，BQ=2．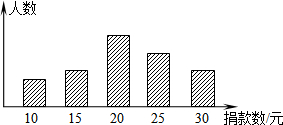
振兴中学某班学生对本校学生会倡导的“助学”捐款活动进行抽样调查，得到了一组学生捐款情况的数据．下图是根据这组数据绘制的统计图，图中从左到右各长方形的高度之比为3：4：8：6：4，又知此次调查中捐款20元和25元的学生共28人．
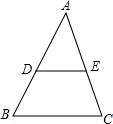如图，△ABC，DE∥BC，若S△ADE：S梯形DBCE=9：16，那么AD：DB=3：2．