题目内容
16. 如图正比例函数y=$\sqrt{3}$x与反比例函数y=$\frac{k}{x}$的图象在第一象限内交于点A,且AO=2,则k等于( )
如图正比例函数y=$\sqrt{3}$x与反比例函数y=$\frac{k}{x}$的图象在第一象限内交于点A,且AO=2,则k等于( )| A. | 1 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 2 |
分析 根据正比例函数的性质求出A的坐标,再根据待定系数法求出k的值.
解答  解:作AD⊥x轴于D.
解:作AD⊥x轴于D.
∵由正比例函数y=$\sqrt{3}$x可知∠AOD=60°,
∵OA=2,
∴OD=1,AD=$\sqrt{3}$
∴A点坐标为(1,$\sqrt{3}$),
将A(1,$\sqrt{3}$)代入数y=$\frac{k}{x}$得:k=1×$\sqrt{3}$=$\sqrt{3}$.
故选B.
点评 此题考查了正比例函数图象上点的坐标特征和用待定系数法求函数解析式,构思巧妙,难度不大.

练习册系列答案
相关题目
6. 如图,利用标杆BE测量树CD的高度,如果标杆BE长为2米,测得AB=3米,AC=9米,且点A、E、D在一条直线上,则树CD是( )
如图,利用标杆BE测量树CD的高度,如果标杆BE长为2米,测得AB=3米,AC=9米,且点A、E、D在一条直线上,则树CD是( )
 如图,利用标杆BE测量树CD的高度,如果标杆BE长为2米,测得AB=3米,AC=9米,且点A、E、D在一条直线上,则树CD是( )
如图,利用标杆BE测量树CD的高度,如果标杆BE长为2米,测得AB=3米,AC=9米,且点A、E、D在一条直线上,则树CD是( )| A. | 6米 | B. | 7.5米 | C. | 8米 | D. | 8.5米 |
7.小婷从标有1到9序号的9张卡片中任意抽取一张,抽到序号是3的倍数的概率是( )
| A. | $\frac{1}{9}$ | B. | $\frac{2}{9}$ | C. | $\frac{1}{3}$ | D. | 1 |
 如图,四边形PMNQ是正方形,△ABC的高AD=6cm,BC=12cm,则正方形PMNQ的边长是4cm.
如图,四边形PMNQ是正方形,△ABC的高AD=6cm,BC=12cm,则正方形PMNQ的边长是4cm.
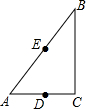 如图,在△ABC中,∠C=90°,AC=6,BC=8,D、E分别是AC、AB的中点.若作半径为8的⊙B,则下列选项中的点在⊙B内的是( )
如图,在△ABC中,∠C=90°,AC=6,BC=8,D、E分别是AC、AB的中点.若作半径为8的⊙B,则下列选项中的点在⊙B内的是( )